Álgebra universitaria

La gráfica de una función cuadrática es una curva en forma de U llamada parábola. Una característica importante del gráfico es que tiene un punto extremo, llamado vértice. Si se abre la parábola, el vértice representa el punto más bajo de la gráfica o el valor mínimo de la función cuadrática. Si la parábola se abre hacia abajo, el vértice representa el punto más alto del gráfico o el valor máximo. En cualquier caso, el vértice es un punto de inflexión en el gráfico. La gráfica también es simétrica con una línea vertical trazada a través del vértice, llamada eje de simetría.

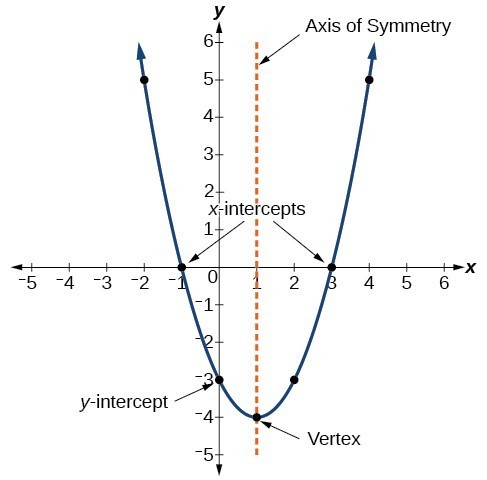
Ecuaciones de funciones cuadráticas

La forma general de una función cuadrática presenta la función en la forma

f \ left (x \ right) = a {x} ^ {2} + bx + c

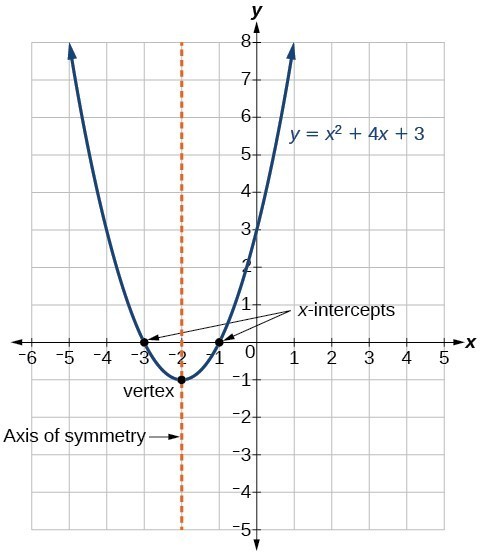
La forma estándar de una función cuadrática presenta la función en la forma

f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k

Dada una función cuadrática en general forma, encuentra el vértice de la parábola.

Una razón por la que podemos querer identificar el vértice de la parábola es que este punto nos informará dónde ocurre el valor máximo o mínimo de la salida, k, y dónde ocurre, h. Si nos dan la forma general de una función cuadrática:

f (x) = ax ^ 2 + bx + c

Podemos definir el vértice, (h, k), haciendo lo siguiente:

Encontrar el dominio y rango de una función cuadrática

Cualquier número puede ser el valor de entrada de una función cuadrática. Por lo tanto, el dominio de cualquier función cuadrática son todos los números reales. Debido a que las parábolas tienen un máximo o un mínimo en el vértice, el rango está restringido. Dado que el vértice de una parábola será un máximo o un mínimo, el rango consistirá en todos los valores de y mayores o iguales a la coordenada y del vértice o menores o iguales a la coordenada y en el punto de inflexión , dependiendo de si la parábola se abre hacia arriba o hacia abajo.

¡Contribuye!

Mejore esta páginaMás información