Algoritmus rychlého řazení

Rychlé řazení je jednou z různých technik řazení, která je založena na konceptu Divide and Conquer, stejně jako Sloučit třídění. Ale v rychlém třídění se vše těžké zvedání (hlavní práce) provádí při dělení pole na subarrays, zatímco v případě sloučení sort se veškerá skutečná práce děje během slučování subarrays. V případě rychlého řazení nedělá krok kombinování absolutně nic.

Nazývá se také řazení podle výměny oddílů. Tento algoritmus rozděluje seznam na tři hlavní části:

1. Prvky menší než prvek Pivot
2. prvek Pivot (centrální prvek)
3. prvky větší než pivotní prvek

Pivotním prvkem může být jakýkoli prvek z pole, může to být první prvek, poslední prvek nebo libovolný náhodný prvek. V tomto tutoriálu vezmeme jako pivot prvek zcela vpravo nebo poslední prvek.

Například: V poli {52, 37, 63, 14, 17, 8, 6, 25} vezmeme 25 jako pivot. Takže po prvním průchodu bude seznam takto změněn.

{6 8 17 14 25 63 37 52}

Proto bude po prvním průchodu pivot nastaven na své místo, přičemž všechny jeho prvky budou nalevo a všechny budou větší než jeho pravé strany. Nyní jsou 6 8 17 14 a 63 37 52 považovány za dva samostatné sluneční paprsky a bude na ně aplikována stejná rekurzivní logika a budeme to dělat, dokud celé pole je tříděno.

Jak funguje rychlé řazení?

Následující kroky zahrnují algoritmus rychlého řazení:

1. Po výběru prvku jako pivot, což je v našem případě poslední index pole, pole poprvé rozdělíme.
2. V rychlém řazení nazýváme toto rozdělení. Není jednoduché rozdělit pole na 2 dílčí pole, ale v případě rozdělení jsou prvky pole umístěny tak, že všechny prvky menší než čep budou na levé straně čepu a všechny prvky větší než čep být na pravé straně.
3. A pivotní prvek bude na své konečné tříděné pozici.
4. Prvky nalevo a napravo nemusí být tříděny.
5. Poté vybereme dílčí pole, prvky nalevo od otočného čepu a prvky napravo od otočného čepu a provedeme rozdělení na nich výběrem otočného čepu v dílčích polích.

Pojďme zvážit pole s hodnotami {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Níže máme obrazové znázornění toho, jak rychlé třídění dané pole seřídí.

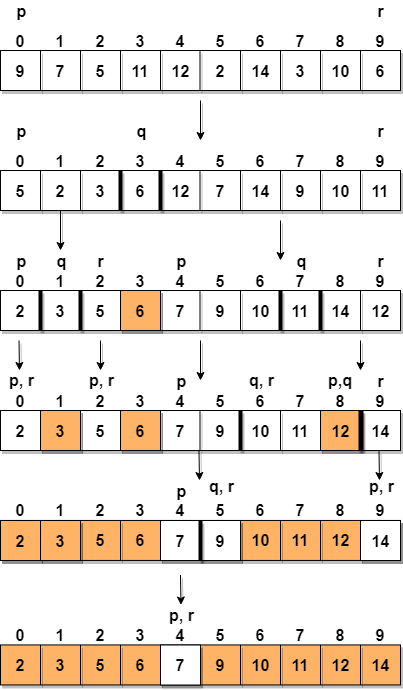
V kroku 1 vybereme poslední prvek jako pivot, což je v tomto případě 6, a volajte po partitioning, proto znovu uspořádejte g pole takovým způsobem, že 6 bude umístěno do své konečné polohy a nalevo budou všechny prvky menší než on a napravo, budeme mít všechny prvky větší než to.

Poté vybereme podpole vlevo a podpole vpravo a vybereme pro ně pivot, ve výše uvedeném diagramu jsme vybrali 3 jako pivot pro levou podskupinu a 11 jako pivot pro pravou podskupinu.

A znovu voláme partitioning.

Implementace algoritmu rychlého řazení

Níže máme jednoduchý program C implementující algoritmus rychlého řazení:

Analýza složitosti rychlého řazení

U pole, ve kterém rozdělení vede k nevyváženým dílčím polím, do té míry, kde na levé straně nejsou žádné prvky se všemi prvky větší než pivot, tedy na pravé straně.

A pokud stále dostáváte nevyvážené dílčí pole, pak běh Nejhorším případem je čas ning, který je O(n2)

Kde jako by rozdělení vedlo k téměř stejným podoblastím, pak je nejlepší doba chodu s časovou složitostí jako O (n * log n).

Nejhorší časová složitost případu: O (n2)

Nejlepší časová složitost případu: O (n * log n)

Průměrná časová složitost: O (n * log n)

Složitost prostoru: O (n * log n)

Jak nyní víme, že pokud dílčí pole vytvoří rozdělení po rozdělení jsou nevyvážené, dokončení rychlého řazení bude trvat déle. Pokud někdo ví, že jste jako pivot vybrali poslední index, může vám úmyslně poskytnout pole, jehož výsledkem bude nejhorší doba běhu pro rychlé řazení.

Chcete-li se tomu vyhnout, můžete vybrat náhodně také otočný prvek. Neurobilo to žádný rozdíl v algoritmu, protože vše, co musíte udělat, je vybrat náhodný prvek z pole, vyměnit jej za prvek na posledním indexu, učinit z něj pivot a pokračovat v rychlém řazení.

• Místo vyžadované rychlým tříděním je mnohem menší, je potřeba pouze O(n*log n) další místo.
• Rychlé řazení není stabilní technika třídění, takže by mohlo během řazení změnit výskyt dvou podobných prvků v seznamu.

Nyní, když jsme se naučili rychlé řazení můžete vyzkoušet i tyto třídicí algoritmy a jejich aplikace:

• Třídění vložení
• Třídění podle výběru
• Řazení podle bublin
• Sloučit řazení
• Heap Sort
• Počítání Seřadit