Poisson-distribution (Svenska)
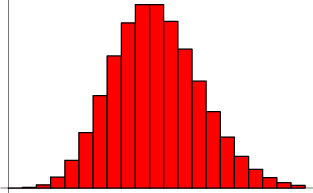
Med tanke på en Poisson-process, är sannolikheten att få exakt 
framgångar i 
prövningar med gränsen för en binomial fördelning
 |
(1)
|
Visar fördelningen som en funktion av det förväntade antalet framgångar
 |
(2)
|
istället för provstorlek 
för fast 
blir ekvation (2) sedan
 |
(3)
|
Låt provstorleken 
bli stor, fördelningen närmar sig sedan
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
som är känd som Poisson-fördelningen (Papoulis 1984, sid 101 och 554; Pfeiffer och Schum 1973, s. 200). Observera att provstorleken 
helt har tappat bort sannolikhetsfunktionen, som har samma funktionella form för alla värden på 
.
Poisson-fördelningen implementeras i WolframLanguage som PoissonDistribution.
Som förväntat normaliseras Poisson-fördelningen så att summan av sannolikheter är lika med 1, eftersom
 |
(9 )
|
Förhållandet mellan sannolikheter ges av
 |
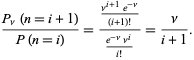(10)
|
Poisson-fördelningen når ett maximum när
 |
(11)
|
där är Euler-Mascheronis konstant och 
är ett harmoniskt tal, vilket leder till den transcendentala ekvationen
 |
(12)
|
som inte kan lösas exakt för 
.
Den momentgenererande funktionen för Poissonsfördelningen ges av
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
så
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, s. 554).
De råa ögonblicken kan också beräknas direkt genom summering, vilket ger en oväntad förbindelse med Bell polynom 
och Stirling-nummer av den andra typen
 |
(21)
|
känd som Dobińskis formel.Därför
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
De centrala momenten kan sedan beräknas som
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
så medelvärdet, variansen, snedheten och kurtosöverskottet är
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
Den karakteristiska funktionen för Poissondistribution är
(Papoulis 1984, s. 154 och 554) och kumuleringsgenereringsfunktionen är
 |
(34)
|
så
 |
(35)
|
Medelavvikelsen för Poisson-fördelningen ges av
 |
(36)
|
Poisson-fördelningen kan också uttryckas i termer av
 |
(37)
|
 |
(38)
|
Den momentgenererande funktionen för aPoisson-fördelning i två variabler ges av
 |
(39)
|
Om de oberoende variablerna 
, 
, …, 
har Poisson-fördelningar med parametrar 
, 
, …, 
, sedan
 |
(40)
|
har en Poisson-distribution med parameter
 |
(41)
|
Detta kan ses eftersom kumuleringsgenereringsfunktionen är
 |
(42)
|
 |
(43)
|
En generalisering av Poisson-fördelningen har använts av Saslaw (1989) för att modellera det observerade klustret av galaxer i universum. Distributionens form ges av
 |
(44)
|
där 
är antalet galaxer i en volym 
, 
, 
är den genomsnittliga densiteten för galaxer, och 
, med 
är förhållandet mellan gravitationsenergi och den kinetiska energi av märkliga rörelser, att låta 
ger
 |
(45)
|
vilket verkligen är en Poisson-distribution med 
. På samma sätt ger 
.