Mätning: Upptäck formler för område

Områdesformler

Studenter som har den informella uppfattningen att området är ”mängden 2-D ”grejer” ”som finns i en region kan själva uppfinna de flesta formler som de ofta bara ombär att memorera. Varje formel de återuppfinner hjälper till att stärka deras förståelse (och minne) för andra formler de känner till. (Se även ytarea.)

Area av rektanglar

Genom att välja en kvadrat som areaenhet får vi en intuitiv uppfattning om arean av rektanglar. Om vi bestämmer att ytan av denna kvadrat är 1, så skulle en rektangel som är 7 gånger så lång ha 7 × 1 som sitt område.

En rektangel som är dubbelt så hög som skulle ha dubbelt så stor yta, så området för är 2 × 7 ytenheter. Vi kan räkna de två raderna med sju rutor. På samma sätt har 3 rader med 7 rutor (eller 7 kolumner med 3 rutor), totalt 7 × 3 rutor, så dess yta är 21 kvadrat enheter.

Antalet rutor i en rad är längden på rektangeln. Antalet rader är rektangelns höjd. Så ytan är längd × höjd.

Eftersom en rektangel kan dras i en lutning definieras ”höjd” som ”riktningen vinkelrät mot basen” och ”bas” definieras som, oavsett vilken sida du väljer att vara.

Det fungerar för att räkna siffror. Det fungerar till och med för bråk. 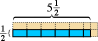Den blå rektangeln som visas här mäter hälften längdenhet hög med fem och hälften längdenheter bred. Om vi väljer motsvarande kvadrat som vår areaenhet ser vi att den blå rektangeln innehåller fem halva enheter yta och en fjärdedel enhet yta, eller en totalt två och tre fjärdedelenheter. (De rosa delarna visar fullbordandet av varje kvadratareaenhet.)

För att inkludera alla siffror definierar vi området för en rektangel som bas × höjd (där ”bas” och ”höjd” betyder längden på dessa sidor, mätt i samma enheter).

Areal för parallellogram

Att få idén

Vi kan räkna ut en formel för ett parallellogram genom dissekering ing parallallogrammet och ordna om delarna för att skapa en rektangel. Eftersom parallellogrammet och rektangeln består av samma delar har de nödvändigtvis samma område. (Se definitionen av område för mer om varför dessa områden är desamma.)

Vi kan se att de också har exakt samma baslängd (blå) och exakt samma höjd (grön). Eftersom bas × höjd ger arean av rektangeln kan vi använda samma mått på parallellogrammet för att beräkna dess area: bas × höjd. (Som tidigare mäts ”höjd” vinkelrätt mot basen och ”bas” är vilken sida du väljer först. Se parallellogram.)

Skäret som visas ovan gör det enkelt att se att baslängden är oförändrad. Faktum är att den vinkelräta skärningen kan göras var som helst längs basen.

Stängning av hålen

Intuition och bevis

Denna dissektion ger en intuitiv förståelse av områdesformeln för ett parallellogram, en anledning att det borde vara vad det är. Men vi har inte ifrågasatt om dissektionen verkligen ”fungerar”. När vi skär parallellogrammet och ordnar om dess delar, förväntar vi oss att få och resultatet ser verkligen ut så. utseende kan vara vilseledande. Vad försäkrar oss om att när vi flyttar den triangeln är resultatet en rektangel? Vad händer om det är mer som (men mindre överdrivet)? Om resultatet inte är alltid en perfekt rektangel, vi kan inte använda vår kunskap om rektangelns områdesformel för att utveckla en formel för parallellogrammet. På gymnasiet kommer eleverna att kunna bevisa att de två delarna av parallellogrammet, när de monteras ordentligt, gör en rektangel I klass K-8 måste eleverna för det mesta förlita sig på det visuella experimentet och få en intuitiv känsla. Läs mer om varför dessa dissektioner fungerar.

Vad händer om vi väljer kortsidan som bas?

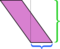
Vi kan välja vilken sida som helst som bas; ”höjd” definieras som mätt vinkelrätt mot den sida vi väljer som bas. Om vi tar kortsidan (blå) som bas, är dissektionen som visas ovan inte lika övertygande. Att klippa längs den höjden och ordna om delarna lämnar en röra:

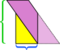
I det här exemplet, vi kan rädda röran genom att göra ytterligare en klippning, 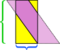men tänk om parallellogrammet var ännu längre och tunnare?

Det visar sig att varje parallellogram, oavsett hur lång och mager, kan dissekeras på detta sätt så att delarna – kanske många av dem – kan ordnas om till en rektangel. Men det krävs mer arbete för att visa att detta alltid kan göras. Vi behöver en annan idé.

En lite annan dissektionsidé gör livet mycket lättare i det här fallet. (På egen hand kan du visa att det också fungerar i originalfallet.)

• Stäng parallellogrammet i en rektangel.
• De två delarna av rektangeln som inte finns inuti parallellogrammet är kongruenta trianglar.
• Skjut en av dessa trianglar mot den andra tills de möts för att bilda en rektangel. 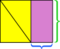Eftersom den totala ytan för den yttre rektangeln inte har ändrats (det är samma rektangel som tidigare) och det gula området har inte förändrats (bitarna har precis flyttat runt), skillnaden mellan dem – de lila områdena – måste vara desamma. Som tidigare kan vi också se att dimensionerna på det rektangulära lila området är basen och höjden på det ursprungliga parallellogrammet.

Intuition och bevis, reprise : Återigen ger dissektionen den väsentliga insikten, men det krävs lite mer arbete för att försäkra att de två gula trianglarna, som verkligen ser ut som om de passar ihop för att göra en rektangel, verkligen passar exakt och inte bara nästan.

Varför är det viktigt att vara så försiktig?

När vi bygger andra områdesformler (nedan) vill vi använda hur vi hittar arean för ett parallellogram, och så vill vi att kunna lita på den regel vi har hittat. Vi kan vara säkra på att omorganisering av delar inte förändrar området: det är ju hur vi definierar område. Men vi måste också vara säkra på att delarna passar ihop som vi hävdar att de gör, eller så kan vi inte lita på de mätningar vi har gjort. Och vi måste vara säkra på att basen × höjdregeln inte beror på ett lyckligt val av bas.

I de flesta läroplaner har eleverna inte en tillräckligt systematisk bas av geometriska kunskaper före klass 8 för att göra ljud bevis på att dessa dissektioner fungerar. Men den intuitiva förståelsen räcker för att förklara och motivera formlerna och en bra grund för senare geometrisk studie.

Triangelarea

Att veta hur man hittar området för ett parallellogram hjälper oss hitta området för en triangel.

Dissekera triangeln

Vi kan dissekera triangeln i två delar – en av dem en triangel och en av dem en trapezoid – genom att skära den parallellt till basen. Om vi skär höjden exakt i hälften med den delen, passar de två delarna ihop för att skapa ett parallellogram med samma bas men hälften av höjden.

Så bas × halvhöjd ger triangelns yta. En liknande dissektion visar halvbas × höjd. Endera av dem minskar till bh.

Fördubbling av triangeln och halvering av det resulterande området

Ett annat sätt att tänka: två kopior av triangeln gör ett parallellogram med samma bas och samma höjd som triangeln.

Parallellogramets area är bas × höjd, men det är dubbelt så mycket som triangelns yta, så triangelns yta är av bas × höjd, som vi såg med dissektionsmetoden.

(Som alltid , välj en ”bas” och mät höjden vinkelrät mot den basen, från basen till motsatta toppunkten.)

Trapezoidens yta

Dubbla trapezoid och halvera sedan det resulterande området

Som det var sant med triangeln kan två kopior av en trapetsform passas ihop för att skapa ett parallellogram.

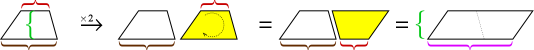
Parallellogrammets höjd är densamma som trapesens höjd, men dess bas är summan av trapesens två baser. Så parallellogramets yta är höjd × (bas1 + bas2). Men det området är två trapezoider, så vi måste skära det på mitten för att få trapezoidens yta.

Dissekera trapezoid

Vi kan också dissekera trapeziden som vi dissekerade triangeln, med en enda skiva som skär sin höjd i hälften. De två delarna passar ihop för att skapa ett parallellogram vars bas är summan av trapesens två baser, men vars höjd är hälften av trapezoidens höjd.

När det gäller trapetsformen kan baserna inte väljas efter behag. De två parallella sidorna är baserna, och höjden är som alltid det vinkelräta avståndet från en bas till motsatsen.

Arealet för detta parallellogram är dess höjd (trapezens halvhöjd) gånger dess bas (summan av trapezens baser), så dess yta är halvhöjd × (bas1 + bas2). Eftersom parallellogrammet är tillverkat av exakt samma ”grejer” som trapesformen, är det också området för trapesformet.

Hur som helst är trapetsformens område × höjd × (bas1 + bas2).

Område för andra speciella fyrkantiga sidor

Område för romben

Området för en rombo kan hittas genom att klippa och ordna om bitarna för att bilda ett parallellogram. Detta kan göras på flera sätt:

1. Klipp över den kortare diagonalen (a) för att bilda två kongruenta trianglar. Flytta den nedre halvan av triangeln bredvid den övre halvan för att bilda ett parallellogram. Den kortare diagonalen (a) blir basen för parallellogrammet och hälften av den längre diagonalen (b) blir parallellogrammets höjd. Således är rombområdet en * b eller produkten av diagonalerna, vilket är standardformeln för romber.
2. Ett annat liknande sätt är att skära romben i fyra kongruenta trianglar och ordna dem till en rektangel med den kortare diagonalen som bas och hälften den längre diagonalen som höjden.
3. Efter skärning romben i två kongruenta trianglar, vi kan beräkna ytan för en av triangeln, som är * bas (a) * höjd ( b) = ab. Multiplicera sedan med två eftersom det finns två av dem: 2 * ab = ab.

Drakarea

Drakens yta kan hittas liknar området för en rombe. Att skära över den längre diagonalen ger två kongruenta trianglar. Om vi ordnar om dem kan vi bilda ett parallellogram med den längre diagonalen (b) som bas och hälften den kortare diagonalen (a) som höjden. Så området blir b * a = ab. Ett mer komplicerat tillvägagångssätt innebär lite algebra. Skär draken över den kortare diagonalen för att bilda två trianglar med den kortare diagonalen (a) som bas. Således är området för den första triangeln a * snurrande, där snurrande är höjden. Området för den andra triangeln är a * (b – squiggly), där (b – squiggly) är den återstående delen av den längre diagonalen. Den totala ytan blir därmed ( a * squiggly) + ( a * (b – squiggly)). Att ta fram a, vi har a (snurrande + b – snurrande) = ab.

Tja, vad vet du. I grund och botten behöver du bara känna till formeln för området för ett parallellogram och sedan härleda formeln för de andra.