Hur man beräknar yta

Beräkningsarea

Area mäts i kvadrater (eller kvadratiska enheter).

Hur många kvadrater finns i denna rektangel?

Vi kan räkna rutorna eller så kan vi ta längd och bredd och använd multiplikation. Rektangeln ovan har en yta på 15 kvadratiska enheter.

Området för en rektangel är = längd x bredd

Exempel på beräkning av arean för en rektangel

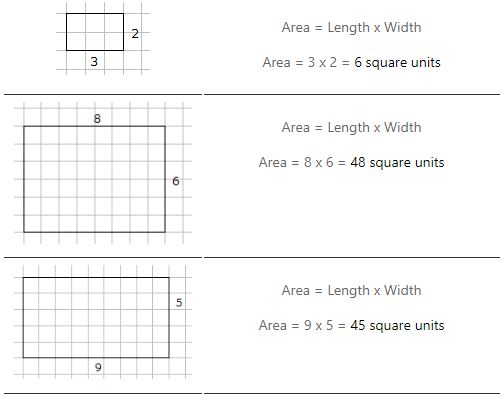
Enheter för mätarea

Vi mäter area med rutor. Vi använder olika storlekar på rutor beroende på hur stort eller litet ett område är.

Exempel	Sidans längd på rutor	Enhet
Storlek på spika på tummen	Millimeter	mm2
Pappersstorlek	Centimeter	cm2
Rummets storlek	Mätare	m2
Storlek på en stad	Kilometer	km2

Glöm inte de små 2

Vi skriver kvadratstorlekar med en liten 2 bredvid enheten.
Vi skriver mm2, cm2, m2, km2, cm2
Vi kan säga ”63 millimeter kvadrat” eller ”63 kvadrat millimeter”

Vi kan använda små rutor för att mäta stora ytor. Det enda problemet med detta är att vi skulle behöva använda mycket stora tal. Till exempel kan ett fält mätas till 5 000 000 000 kvadratmillimeter när 5 000 kvadratmeter skulle vara mycket lättare att säga, skriva och visualisera.

Du kommer förmodligen att höra fler enheter för mätarea; kvadratcentimeter, kvadratfot, kvadratmeter, kvadratkilometer, tunnland, hektar är alla enheter som används för att mäta område.

Fler exempel på beräkning av areal

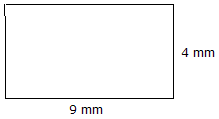	Area = Längd x Bredd Area = 9 mm x 4 mm = 36 mm2
	Area = Längd x Bredd Area = 7 cm x 6 cm = 42 cm2
	Area = Längd x Bredd Area = 8 mx 2 m = 16 m2
	Area = Längd x Bredd Area = 7 km x 5 km = 35 km2

Område för en kvadrat

En kvadrats längd och bredd är desamma så vi behöver bara multiplicera längden med längden.

Area = Längd x Längd Area = 6 cm x 6 cm = 36 cm2

Område för en cirkel

Området för en cirkel = πr2
där r är cirkelns radie och π är förhållandet mellan en cirkels omkrets och dess diameter.

π (uttalas ”pie” och ofta skrivet ”Pi”) är en oändlig decimal med ett gemensamt ungefärlig 3.14159. Du kan läsa mer om Pi här

Exempel på beräkning av en cirkels area

Area = πr2 Area = 3.14159 x (4 cm) 2 Area = 3.14159 x 16 cm2 Area = 50.27 cm2 Svar avrundat till 2 decimaler

Förklaring av området för en cirkelformel

Ta en cirkel och dela den i lika stora sektorer och ordna om dem enligt nedan. Lägg märke till hur, när sektorerna blir mindre, formen blir mer som en rektangel. Obs! Det finns ingen gräns för hur små dessa sektorer kan vara och hur nära de kan likna en rektangel när de är ordnade.

Förutsatt att vi vet att omkretsen av en cirkel är lika med 2πr kan vi lägga till dimensioner till ”rektangeln” som visas nedan. Med hjälp av området för en rektangelformel, area = bredd x höjd kan vi se hur vår cirkel, omkonfigurerad som en rektangel, kan visas att ha ett område som approximerar till πr xr eller πr2

Cirkel Sektorer omarrangerade

Cirkelsektorer omarrangerade – startar att se ut som en rektangel

Område för Sammansatta former

Det finns många fall där beräkningen av en total yta kräver att mer än ett område beräknas följt av antingen ett tillägg, subtrahering eller någon annan kombination av operationer för att hitta önskat område.

Obs: I exemplen nedan visas inte måttenheterna och svar och värdet på π (Pi) har avrundats till närmaste hundradel.

Exempel: Enkla sammansatta former

Exempel på areaberäkning nedan är relativt enkelt. Formen kan ses som en triangel i kombination med en rektangel.

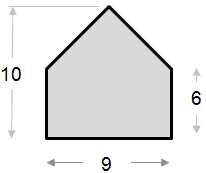Area av triangeldel: ½ x bas x höjd ½ x 9 x 4 = 18 Rektangelens area: bredd x höjd 9 x 6 = 54 Total yta = 18 + 54 = 72

Exemplet ovan illustrerar ett vanligt krav när man arbetar med förening former – hitta dimensioner som inte visas. När du undervisar dina barn, ge hjälp, när det behövs, för att hitta dessa ”saknade” dimensioner. Det finns ett annat exempel nedan.

Hitta måtten

Vilka mått har den lilla rektangulära delen? Bredd? 12 – 7 – 2 = 3 Höjd? 8 – 6 = 2

Exempel: subtrahera ett område från ett annat

I exemplet nedan kan formen ses som en rektangel med en triangel utskuren.

Area av rektangeldel: bredd x höjd 5 x 6 = 30 Area av triangeldel: ½ x bas x höjd ½ x 3 x 3 = 4,50 Total yta = 30 – 4,50 = 25,50

Exempel: Delarea

Exemplet nedan liknar en ovan, men eftersom vi har en halvcirkel måste vi beräkna en bråkdel (hälften) av cirkelns område. Observera i detta exempel diametern och inte radien.

Area av triangeldel: ½ x bas x höjd ½ x 6 x 6 = 18 Area av halvcirkeldel: ½ x (πr2) ½ x (3.14 x 1,52) = 3,53 Total yta = 18 – 3,53 = 14,47

Exempel: Beslut! Kombinera? Subtrahera

Det är vanligt att man har mer än ett sätt att beräkna det slutliga området. I exemplen nedan kan formen ses som två rektanglar i kombination eller som en stor rektangel med en mindre rektangel som ”klipps ut” från det övre högra hörnet.

Beräkning av arbetsblad

Skriv ut ta reda på kalkylbladen nedan och använd dem för att träna dina barn.

• Beräkna områden – rektanglar och rutor
• Beräkna områden – rektanglar
• Beräkna Områden – Rektanglar
• Beräkning av sammansatta områden t.ex. med rektangulära former
• Beräkna sammansatta ytor t.ex. med rektanglar, trianglar och cirklar
• Beräkna områden t.ex. av trianglar
• Area of a Circle
• Beräkning av ytarea t.ex. av rektangulära prismer

Du hittar fler utskriftsbara geometriska kalkylblad här.