Hur man beräknar volymen

Beräknar volymen

Volymen mäts i kuber (eller kubiska enheter).

Hur många kuber finns i detta rektangulära prisma (kuboid)?

Vi kan räkna kuberna, även om det är snabbare att ta längd, bredd och höjd och använda multiplikation. Det rektangulära prisma ovan har en volym av 48 kubik enheter.

Volymen för ett rektangulärt prisma är = längd x bredd x höjd

Exempel på beräkning av arean för en rektangel

Vi måste göra två multiplikationer för att räkna ut volymen. Vi beräknar ytan på ett ansikte (eller sida) och multiplicerar det med dess höjd. Exemplen nedan visar hur det finns tre sätt att göra detta.

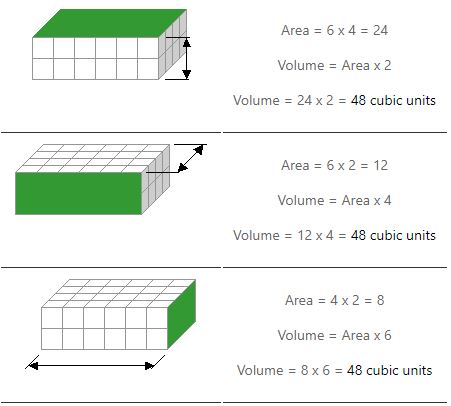
Lägg märke till hur vi får samma svar oavsett vilken sida vi använder för att hitta ett område.

När ditt barn börjar arbeta med yta och omkrets kommer han eller hon vanligtvis att arbeta med två dimensioner – rutor, rektanglar, trianglar etc. som visas på papper som platta – det finns inget djup eller 3: e dimension. Att arbeta med volym innefattar tre dimensioner. Se till att ditt barn är medveten om detta och inte tänker på kuber och andra 3D-former som visas på papper som bara en annan ”form på sidan”. Visa dem riktiga rutor och visa hur dessa kan ritas (eller representeras) på ett tvådimensionellt papper. Med andra ord, se till att kopplingen mellan vad som står på papper och vad den representerar i den verkliga världen skapas.

Var noga med att ditt barn inte är förvirrad av användningen av volymen som används när man talar om ljud .

Enheter för mätning av volym

Det finns mycket stora skillnader mellan måttenheter för volym. Till exempel finns det 100 centimeter på 1 meter men det finns 1 000 000 (ja, 1 miljon ) kubikcentimeter i en kubikmeter.

Varför den stora skillnaden? För i volym har vi inte bara längd, vi har längd, bredd och höjd. Sockerkubsexemplet nedan visar detta.

Hur mycket socker? 1 m3 eller 1.000.000 cm3

Tänk på att fylla en mycket stor låda (den skulle vara 1 meter bred, 1 meter, lång och en meter hög) med sockerbitar (med vardera sida 1 centimeter).

	Steg 1: en rad längs botten av rutan – det skulle vara 100 sockerbitar
	Steg 2: täck resten av lådans botten – vilket ger totalt 100 rader vardera med 100 sockerbitar. 100 x 100 = 10 000 socker och kuber längst ner i den stora lådan.
	Steg 3: Upprepa detta 99 gånger tills det finns lager med 10.000 kuber staplade 100 djupa. 10.000 x 100 = 1.000.000 sockerbitar

Det finns 1 000 000 cm3 i 1 m3 – var försiktig så att du inte har för mycket socker!

Det finns andra enheter för att mäta volym; kubikcentimeter, kubikfot, kubikmeter är alla enheter som används för att mäta volym. Milliliter, liter, gallon används också speciellt vid mätning av vätskor.

Glöm inte wee 3

Vi skriver kubikstorlekar med en liten 3 bredvid enheten.
Vi skriver mm3, cm3, m3, km3, cm3
Vi kan säga ”85 centimeter kubad” eller ”85 kubikcentimeter”

Exempel på beräkning av volym rektangulära prismer

	Volym = Längd x Bredd x Höjd Volym = 12 cm x 8 cm x 6 cm = 576 cm3
	Volym = Längd x Bredd x Höjd Volym = 20 mx 2 mx 2 m = 80 m3
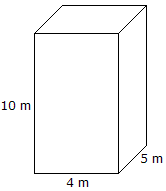	Volym = Längd x Bredd x Höjd Volym = 10 mx 4 mx 5 m = 200 m3

Volym av en cylinder

Beräkning av volymen för en cylinder der innebär att multiplicera ytan på basen med cylinderns höjd. Basen på en cylinder är cirkulär och formeln för en cirkels yta är: area av en cirkel = πr2. Det finns mer här på området för en cirkel.

Volym = Basyta x Höjd Volym = πr2 xh Volym = πr2 h

Obs: i exemplen nedan vi kommer att använda 3.14 som ett ungefärligt värde för π (Pi).

Exempel på beräkning av volymen för en cylinder

Måtten är i cm.

Volym = πr2 h Volym = 3.14 x 3 x 3 x 8 Volym = 226,08 cm3

En kons volym

En kons volym är lika med en tredjedel av volymen på en cylinder med matchande höjd och basarea. Detta ger formeln för volymen på en kon som visas nedan.

Volym = 1/3 πr2h

Exempel på beräkning av volymen på en kon

Mått är i cm.

Volym = 1/3 πr2 h Volym = 1/3 x 3,14 x 2 x 2 x 7 Volym = 29,31 cm3

Volym av en sfär

Formeln för en sfärs volym visas nedan.

Volym = 4/3 πr3

Exempel på beräkning av en sfärvolym

Måtten är i cm.

Volym = 4/3 πr3 Volym = 4/3 x 3,14 x 4 x 4 x 4 Volym = 267,95 cm3

Utskrivbara volymkalkylblad

Använd kalkylbladet nedan för att öva på att beräkna volymer.

• Hitta volym i kubiska enheter – rektangulära prismer och kompositer
• Volymer av rektangulära prismer
• Volymer av rektangulära prismer
• Volymer av ”verkliga” objekt t.ex. av spannmålslådor
• Beräkna volymer t.ex. av triangulära prismer och cylindrar

Du får andra geometriska kalkylblad i omkrets, område och mer här.