Exponentiell fördelning
av Marco Taboga, doktor
Den exponentiella fördelningen är en kontinuerlig sannolikhetsfördelning som används för att modellera den tid vi behöver vänta innan en viss händelse inträffar. Det är den kontinuerliga motsvarigheten till den geometriska fördelningen, som istället är diskret.
Ibland kallas den också negativ exponentiell fördelning.
Inledning
Hur mycket tid kommer det att gå innan en jordbävning inträffar i en viss region? Hur länge behöver vi vänta tills en kund kommer in i vår butik? Hur lång tid tar det innan ett callcenter tar emot nästa telefonsamtal? Hur länge kommer en maskin att fungera utan att gå sönder?
Frågor som dessa besvaras ofta i probabilistiska termer med hjälp av den exponentiella fördelningen.
Alla dessa frågor gäller den tid vi behöver att vänta innan en viss händelse inträffar. Om denna väntetid är okänd är det ofta lämpligt att tänka på den som en slumpmässig variabel som har en exponentiell fördelning.
Grovt sagt, tiden 
att vänta innan en händelse inträffar har en exponentiell fördelning om sannolikheten för att händelsen inträffar under ett visst tidsintervall är proportionell mot längden på det tidsintervallet.
Mer exakt, har en exponentiell fördelning om den villkorliga sannolikheten är ungefär proportionell mot längden för tidsintervallet mellan tidpunkterna och , för vilken som helst ögonblick .
I många praktiska situationer är denna egenskap väldigt realistisk. Detta är anledningen till att den exponentiella fördelningen används så ofta för att modellera väntetider.
Den exponentiella fördelningen är strikt relaterad till Poisson-distributionen. Om 1) en händelse kan inträffa mer än en gång och 2) tiden mellan två på varandra följande händelser är exponentiellt fördelad och oberoende av tidigare händelser, så har antalet händelser inom en given tidsenhet en Poisson-fördelning. Vi inbjuder läsaren att se föreläsningen om Poisson-distributionen för en mer detaljerad förklaring och en intuitiv grafisk framställning av detta faktum.
Definition
Den exponentiella fördelningen kännetecknas enligt följande.
Definition Låt vara en kontinuerlig slumpmässig variabel. Låt dess stöd vara en uppsättning positiva reella tal: Låt . Vi säger att har en exponentiell fördelning med parametern om och endast om dess sannolikhetsdensitetsfunktion är Parametern kallas hastighetsparameter.
En slumpmässig variabel med en exponentiell fördelning kallas också en exponentiell slumpmässig variabel.
Följande är ett bevis på att är en legitim sannolikhetsdensitetsfunktion.
Icke-negativitet är uppenbart. Vi måste bevisa att integralen av över är lika med . Detta bevisas enligt följande:
För att bättre förstå den exponentiella fördelningen kan du titta på dess densitetsdiagram.
Hastighetsparametern och dess tolkning
Vi har nämnt att sannolikheten för att händelsen inträffar mellan två datum och är proportionell mot (villkorad av att den inte har förekommit före ). Hastighetsparametern är proportionalitetskonstanten: där är ett oändligt högre ordning än (dvs. en funktion av som går till noll snabbare än gör).
Ovanstående proportionalitetsvillkor är också tillräckligt för att fullständigt karakterisera den exponentiella fördelningen.
Proposition Proportionalitetsvillkoret uppfylls endast om har en exponentiell fördelning.
Den villkorliga sannolikheten kan skrivas som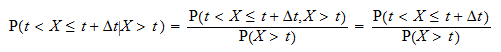 
Beteckna med fördelningsfunktionen för , det vill säga och av dess överlevnadsfunktion: Därefter Dela båda sidor med , vi får där är en kvantitet som tenderar att när tenderar att . Att ta gränser på båda sidor får vi eller, genom definitionen av derivat: Denna differentialekvation löses enkelt med kedjan regel: Att ta integralen från till på båda sidor får vi och eller Men (eftersom inte kan ta negativa värden) innebär att Exponentierar båda sidor, vi får Därför eller Men densitetsfunktionen är det första derivatet av fördelningsfunktionen: och termen längst till höger är densiteten hos en exponentiell slumpmässig variabel. Därför är proportionalitetsvillkoret endast uppfyllt om är en exponentiell slumpmässig variabel
Förväntat värde
Det förväntade värdet för en exponentiell slumpmässig variabel är
Det kan härledas enligt följande: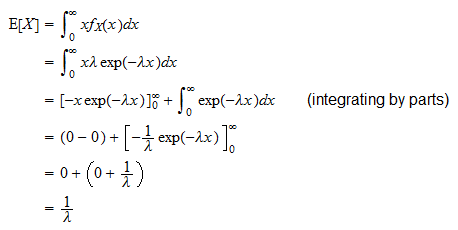 
Varians
Variansen för en exponentiell slumpmässig variabel är
Det kan härledas tack vare den vanliga variansformeln (): 
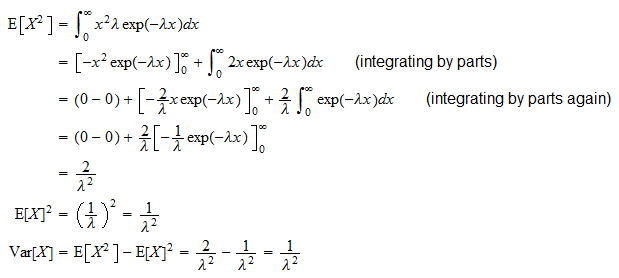
Momentgenererande funktion
Momentgenereringsfunktionen för en exponentiell slumpmässig variabel definieras för alla :
Definitionen av momentgenererande funktion ger Av Naturligtvis konvergerar ovanstående integraler bara om , dvs bara om . Därför existerar den momentgenererande funktionen för en exponentiell slumpmässig variabel för alla .
Karaktäristisk funktion
Den karakteristiska funktionen för en exponentiell slumpmässig variabel är
Genom att använda definitionen av karakteristisk funktion och det faktum att kan vi skriva Vi beräknar nu de två integralerna separat . Den första integralen är 
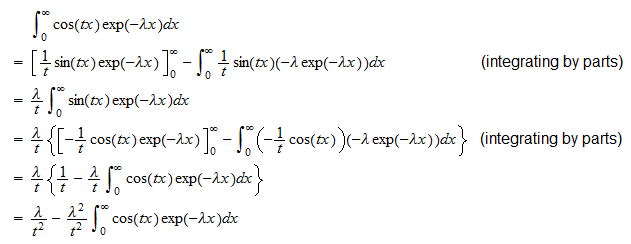Därför som kan ordnas om för att ge eller Den andra integralen är 
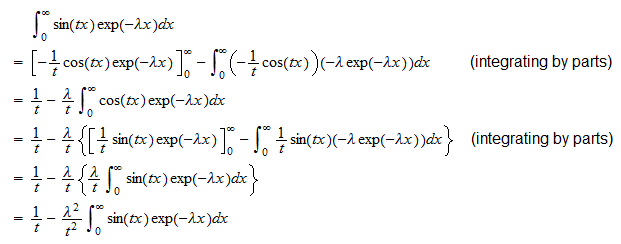Därför som kan ordnas om för att ge eller Genom att sätta ihop bitar får vi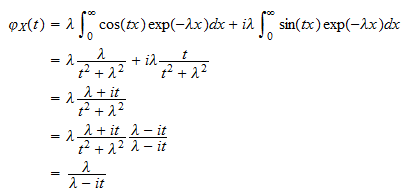 
Distributionsfunktion
Distributionsfunktionen för en exponentiell slumpmässig variabel är
Om , då eftersom kan inte ta negativa värden. Om , så
Mer information
I följande underavsnitt kan du hitta mer information om den exponentiella fördelningen.
Minneslös egenskap
En av de viktigaste egenskaperna för den exponentiella fördelningen är den minneslösa egenskapen: för alla .
Detta bevisas enligt följande: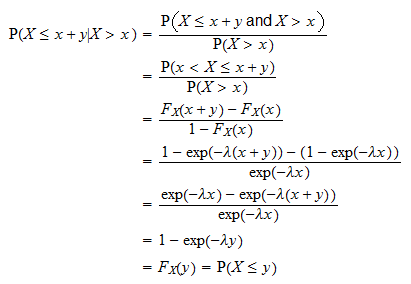 
är tiden vi behöver vänta innan en viss händelse inträffar. Ovanstående egenskap säger att sannolikheten för att händelsen inträffar under ett tidsintervall med längden är oberoende av hur mycket tid som redan har gått () utan att händelsen inträffar.
Summan av exponentiella slumpmässiga variabler är en Gamma-slumpvariabel
Antag att , , …, är ömsesidigt oberoende slumpmässiga variabler med exponentiell fördelning med parameter .
Definiera
Sedan är summan en Gamma-slumpmässig variabel med parametrar och .
Detta bevisas med hjälp av moment generera funktioner (kom ihåg att momentgenereringsfunktionen för en summa av ömsesidigt oberoende slumpmässiga variabler bara är produkten av deras momentgenererande funktioner): Den senare är den momentgenererande funktionen för en Gamma distribution med parametrar och . Så har en gammafördelning, eftersom två slumpmässiga variabler har samma fördelning när de har samma momentgenererande funktion.
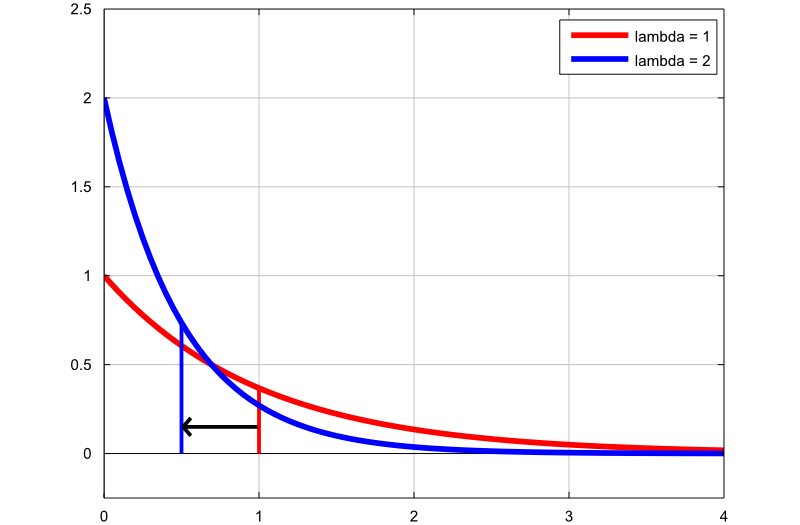
Den slumpmässiga variabeln sägs också ibland ha en Erlang-distribution. Erlang-fördelningen är bara ett speciellt fall för gammafördelningen: en gammal slumpmässig variabel är också en Erlang-slumpvariabel när den kan skrivas som en summa av exponentiella slumpmässiga variabler. p> Nästa plot visar hur densiteten hos den exponentiella fördelningen ändras genom att ändra hastighetsparametern:
-
den första grafen (röd linje) är sannolikhetsdensitetsfunktionen för en exponentiell slumpmässig variabel med hastighetsparameter
; -
den andra grafen (blå linje) är sannolikhetsdensitetsfunktionen för en exponentiell slumpmässig variabel med hastighetsparameter
.
De tunna vertikala linjerna anger medel för de två fördelningarna. Observera att genom att öka hastighetsparametern minskar vi medelvärdet för fördelningen från till .
Lösta övningar
Nedan hittar du några övningar med förklarade lösningar.
Övning 1
Låt vara en exponentiell slumpmässig variabel med parametern . Beräkna följande sannolikhet:
Först och främst kan vi skriva sannolikheten som med användning av det faktum att sannolikheten för att en kontinuerlig slumpmässig variabel får ett visst värde är lika med noll (se Kontinuerliga slumpmässiga variabler och noll-sannolikhetshändelser). Nu kan sannolikheten skrivas i termer av fördelningsfunktionen för som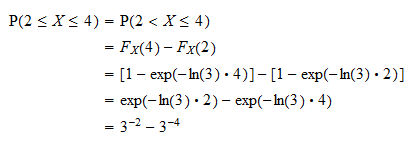 
Övning 2
Antag att den slumpmässiga variabeln har en exponentiell fördelning med parametern . Beräkna följande sannolikhet:
Denna sannolikhet kan enkelt beräknas med hjälp av fördelningsfunktionen för :
Övning 3
Vad är sannolikheten för att en slumpmässig variabel är mindre än det förväntade värdet, om har en exponentiell fördelning med parametern ?
Det förväntade värdet för en exponentiell slumpmässig variabel med parametern är Sannolikheten ovan kan beräknas med hjälp av fördelningsfunktionen för :
Hur man citerar
Vänligen citera som: