College-algebra (Svenska)
Inlärningsresultat
- Identifiera toppunkt, symmetriaxel, y-skärning och minimi- eller maximivärde för en parabel från dess diagram.
- Identifiera en kvadratisk funktion skriven i allmän och vertexform.
- Med en kvadratisk funktion i allmän form, hitta toppunkten.
- Definiera domänen och räckvidd för en kvadratisk funktion genom att identifiera toppunkten som ett maximum eller minimum.
Grafen för en kvadratisk funktion är en U-formad kurva som kallas en parabel. En viktig funktion i grafen är att den har en extrem punkt, kallad toppunkt. Om parabolen öppnas representerar toppunkten den lägsta punkten i diagrammet, eller minimivärdet för den kvadratiska funktionen. Om parabolen öppnar sig representerar toppunkten den högsta punkten i diagrammet, eller det maximala värdet. I båda fallen är toppunkten en vändpunkt i diagrammet. Grafen är också symmetrisk med en vertikal linje som dras genom toppunkten, kallad symmetriaxel.
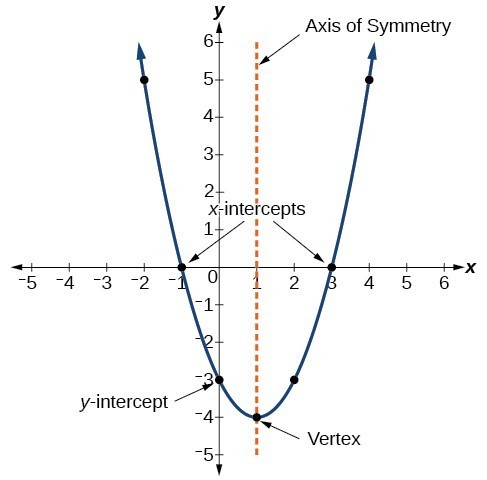
Ekvationer av kvadratiska funktioner
Den allmänna formen av en kvadratisk funktion presenterar funktionen i formen
f \ left (x \ right) = a {x} ^ {2} + bx + c
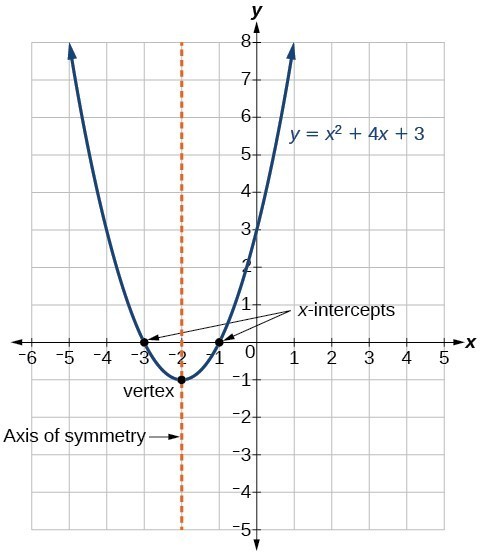
Standardformen för en kvadratisk funktion presenterar funktionen i formen
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Givet en kvadratisk funktion i allmänhet form, hitta parabolens topp.
En anledning till att vi kanske vill identifiera toppunkten för parabolen är att denna punkt kommer att informera oss om det maximala eller minsta värdet för utdata sker, k och var det inträffar, h. Om vi får den allmänna formen av en kvadratisk funktion:
f (x) = ax ^ 2 + bx + c
Vi kan definiera toppunkten, (h, k), genom att göra följande:
Hitta domänen och räckvidden för en kvadratisk funktion
Vilket som helst tal kan vara ingångsvärdet för en kvadratisk funktion. Därför är domänen för varje kvadratisk funktion alla reella tal. Eftersom parabolor har ett maximalt eller ett minimum vid toppunkten är räckvidden begränsad. Eftersom toppunkten för en parabel kommer att vara antingen ett maximalt eller ett minimum, kommer intervallet att bestå av alla y-värden större än eller lika med y-koordinaten för toppunkten eller mindre än eller lika med y-koordinaten vid vändpunkten , beroende på om parabolen öppnas eller sänks.
Bidra!
Förbättra den här sidanLäs mer