Măsurare: descoperirea formulelor pentru zonă

Formule pentru zonă

Studenții care au noțiunea informală că aria este „cantitatea de 2-D „chestii” ”conținute în interiorul unei regiuni pot inventa singuri majoritatea formulelor pe care li se cere adesea doar să le memoreze. Fiecare formulă pe care o reinventează ajută la întărirea înțelegerii (și a memoriei) pentru celelalte formule pe care le cunosc. (A se vedea și suprafața.)

Zona dreptunghiurilor

Alegând un pătrat ca unitate de suprafață, avem o idee intuitivă despre aria dreptunghiurilor. Dacă decidem că aria acestui pătrat este 1, atunci un dreptunghi care este de 7 ori mai lung ar avea 7 × 1 ca zonă.

Un dreptunghi care este de două ori înălțimea ar avea de două ori aria sa, deci aria este 2 × 7 unități de suprafață. Putem număra cele două rânduri de șapte pătrate. În mod similar, are 3 rânduri de 7 pătrate (sau 7 coloane de 3 pătrate), pentru un total de 7 × 3 pătrate, deci aria sa este de 21 de unități pătrate.

Numărul de pătrate dintr-un rând este lungimea dreptunghiului. Numărul de rânduri este înălțimea dreptunghiului. Deci, aria este lungimea × înălțimea.

Deoarece un dreptunghi poate fi trasat la o înclinare, „înălțimea” este definită pentru a însemna „direcția perpendiculară pe bază” și „baza” este definită ca fiind, Ei bine, indiferent de partea pe care o alegeți.

Aceasta funcționează pentru numărarea numerelor. Funcționează chiar și pentru fracțiuni. 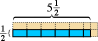Dreptunghiul albastru afișat aici măsoară jumătate lungime-unitate înălțime cu cinci și jumătate de lungime-unități. Dacă alegem pătratul corespunzător ca unitate de suprafață, vedem că dreptunghiul albastru conține cinci jumătăți de unități de suprafață și un sfert de unitate de suprafață, sau o total de două și trei sferturi de unități de suprafață. (Părțile roz arată finalizarea fiecărei unități de suprafață pătrată.)

Pentru a include toate numerele, definim aria unui dreptunghi care să fie bază × înălțime (unde „bază” și „înălțime” înseamnă lungimile acelor laturi, măsurate în aceleași unități).

Zona paralelogramelor

Obținerea ideii

Putem afla o formulă pentru aria unui paralelogram prin disecție paralelogramul și rearanjarea părților pentru a face un dreptunghi. Deoarece paralelogramul și dreptunghiul sunt compuse din aceleași părți, ele au în mod necesar aceeași zonă. (A se vedea definiția zonei pentru mai multe informații despre motivul pentru care acele zone sunt aceleași.)

Putem vedea că și ele au exact aceeași lungime a bazei (albastru) și exact aceeași înălțime (verde). Deoarece baza × înălțimea dă aria dreptunghiului, putem folosi aceleași măsurători pe paralelogram pentru a calcula aria sa: baza × înălțimea. (La fel ca înainte, „înălțimea” se măsoară perpendicular pe bază, iar „baza” este oricare parte ați ales mai întâi. Vedeți paralelogramul.)

Tăierea prezentată mai sus face ușor de văzut că lungimea bazei este neschimbat. De fapt, tăierea perpendiculară poate fi făcută oriunde de-a lungul bazei.

Îngrijirea găurilor

Intuiție și dovadă

Această disecție oferă o înțelegere intuitivă a formulei zonei pentru un paralelogram, motiv pentru care ar trebui să fie ceea ce este. Dar nu ne-am pus la îndoială dacă disecția „funcționează cu adevărat”. Adică, atunci când tăiem paralelogramul și rearanjăm părțile sale, ne așteptăm să obținem și rezultatul cu siguranță arată așa. Dar aparențele pot fi înșelătoare. Ce ne asigură că atunci când mutăm acel triunghi, rezultatul este un dreptunghi? Ce se întâmplă dacă seamănă mai mult cu (deși mai puțin exagerat)? Dacă rezultatul nu este întotdeauna un dreptunghi perfect, nu putem folosi cunoștințele noastre despre formula ariei dreptunghiului pentru a dezvolta o formulă pentru paralelogram. În liceu, elevii vor putea demonstra că cele două părți ale paralelogramului, atunci când sunt reasamblate corect, fac un dreptunghi . În clasele K-8, în mare parte, elevii trebuie să se bazeze pe experimentul vizual și să aibă o senzație intuitivă. Aflați mai multe despre de ce funcționează aceste disecții.

Ce se întâmplă dacă alegem partea scurtă ca bază?

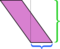
Suntem liberi să alegem orice parte ca bază; „înălțime” este definit a fi măsurată perpendicular pe latura pe care o alegem ca bază. Dacă luăm ca bază partea scurtă (albastră), disecția de mai sus nu este la fel de convingătoare. Tăierea de-a lungul acelei altitudini și rearanjarea părților lasă o mizerie:

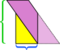
În acest exemplu particular, putem salva mizeria făcând încă o tăietură, 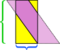dar dacă paralelogramul ar fi și mai lung și mai slab?

Se pare că orice paralelogram, oricât de lung și slab, poate fi disecat în acest fel, astfel încât părțile – poate multe dintre ele – să poată fi rearanjate într-un dreptunghi. Dar este nevoie de mai multă muncă pentru a arăta că acest lucru se poate face întotdeauna. Avem nevoie de o altă idee.

O idee de disecție ușor diferită facilitează viața în acest caz. (Pe cont propriu, puteți arăta că funcționează și în cazul original.)

• Încadrați paralelogramul într-un dreptunghi.
• Cele două părți ale dreptunghiului care nu se află în interiorul paralelogramului sunt triunghiuri congruente.
• Glisați unul dintre aceste triunghiuri către celălalt până când se întâlnesc pentru a forma un dreptunghi. 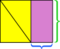Deoarece aria totală a dreptunghiului exterior nu s-a schimbat (este același dreptunghi ca înainte) și zona galbenă nu s-a schimbat (piesele tocmai s-au deplasat), diferența dintre ele – zonele mov – trebuie să fie aceleași. Ca și înainte, putem vedea, de asemenea, că dimensiunile zonei violet dreptunghiulare sunt baza și înălțimea paralelogramului original.

Intuiție și dovadă, repetare : Din nou, disecția oferă o perspectivă esențială, dar este nevoie de un pic mai mult de lucru pentru a se asigura că cele două triunghiuri galbene, care cu siguranță parcă s-ar potrivi împreună pentru a forma un dreptunghi, se potrivesc cu adevărat exact și nu doar aproape.

De ce este important să fim atât de atenți?

Când construim alte formule de zonă (mai jos), vom dori să folosim modul nostru de a găsi aria unui paralelogram, așa că dorim să ne putem baza pe regula pe care am găsit-o. Putem fi siguri că rearanjarea pieselor nu schimbă zona: acesta este, la urma urmei, modul în care definim zona. Dar trebuie, de asemenea, să fim siguri că piesele se potrivesc așa cum pretindem că fac sau nu ne putem baza pe măsurătorile pe care le-am făcut. Și trebuie să fim siguri că regula bază × înălțime nu depinde de o alegere norocoasă de bază.

În majoritatea programelor, elevii nu au o bază sistematică suficientă de cunoștințe geometrice înainte de clasa a 8-a pentru a face dovezi solide că aceste disecții funcționează. Dar înțelegerea intuitivă este suficientă pentru a explica și a justifica formulele și o bază bună pentru un studiu geometric ulterior.

Zona triunghiului

Știind cum să găsim aria unui paralelogram ne ajută găsiți aria unui triunghi.

Disecarea triunghiului

Putem diseca triunghiul în două părți – una dintre ele un triunghi, iar una dintre ele un trapez – prin tăiere paralelă până la bază. Dacă tăiem înălțimea exact în jumătate cu acea felie, cele două părți se potrivesc împreună pentru a face un paralelogram cu aceeași bază, dar jumătate din înălțime.

Deci baza × jumătate-înălțime dă aria triunghiului. O disecție similară arată jumătate de bază × înălțime. Oricare dintre ele se reduce la bh.

Dublând triunghiul și apoi înjumătățind aria rezultată

Un alt mod de gândire: două copii ale triunghiul face un paralelogram cu aceeași bază și aceeași înălțime ca triunghiul.

Zona paralelogramului este baza × înălțimea, dar aceasta este de două ori aria triunghiului, deci aria triunghiului este de bază × înălțime, așa cum am văzut cu metoda de disecție.

(Ca întotdeauna , alegeți o „bază” și măsurați înălțimea perpendiculară pe acea bază, de la bază la vârful opus.)

Zona trapezului

Dublând trapezul și apoi înjumătățind aria rezultată

Așa cum a fost adevărat cu triunghiul, două copii ale unui trapez pot fi potrivite împreună pentru a face un paralelogram.

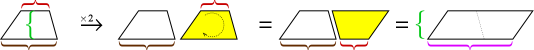
Înălțimea paralelogramului este aceeași cu înălțimea trapezului, dar baza acestuia este suma celor două baze ale trapezului. Deci aria paralelogramului este înălțimea × (baza1 + baza2). Dar acea zonă este de două trapezoide, deci trebuie să o tăiem în jumătate pentru a obține aria trapezului.

Disecarea trapezului

Am putea diseca și trapezul așa cum am disecat. triunghiul, cu o singură felie, tăindu-și înălțimea în jumătate. Cele două părți se potrivesc împreună pentru a face un paralelogram a cărui bază este suma celor două baze ale trapezului, dar a căror înălțime este jumătate din înălțimea trapezului.

În cazul trapezului, bazele nu pot să fie ales după bunul plac. Cele două laturi paralele sunt bazele, iar înălțimea, ca întotdeauna, este distanța perpendiculară de la o bază la opus.

Aria acestui paralelogram este înălțimea sa (jumătate-înălțime a trapezului) de ori mai mult decât baza sa (suma bazelor trapezului), deci aria sa este de jumătate înălțime × (baza1 + baza2). Deoarece paralelogramul este realizat exact din același „material” ca și trapezul, aceasta este și zona trapezului.

În orice caz, aria trapezului este × înălțime × (bază1 + bază2).

Zona altor patrulatere speciale

Zona rombului

Zona unui romb poate fi găsită prin tăierea și rearanjarea pieselor pentru a forma un paralelogram. Acest lucru se poate face în mai multe moduri:

1. Tăiați diagonala mai scurtă (a) pentru a forma două triunghiuri congruente. Mutați jumătatea inferioară a triunghiului de lângă jumătatea superioară pentru a forma un paralelogram. Diagonala mai scurtă (a) devine baza paralelogramului, iar jumătatea diagonalei mai lungi (b) devine înălțimea paralelogramului. Astfel, zona rombului este un * b sau produsul diagonalelor, care este formula standard pentru romb.
2. O altă modalitate similară este tăierea rombului în patru triunghiuri congruente și rearanjarea lor într-un dreptunghi cu diagonala mai scurtă ca bază și jumătate din diagonala mai lungă ca înălțime.
3. După tăiere rombul în două triunghiuri congruente, putem calcula aria unuia dintre triunghiuri, care este * bază (a) * înălțime ( b) = ab. Apoi, înmulțiți-vă cu două, deoarece există două dintre ele: 2 * ab = ab.

Zona zmeului

Zona zmeului poate fi găsită similar cu zona unui romb. Tăierea peste diagonala mai lungă dă două triunghiuri congruente. Dacă le rearanjăm, putem forma un paralelogram cu diagonala mai lungă (b) ca bază și jumătate din diagonala mai scurtă (a) ca înălțime. Deci, zona devine b * a = ab. O abordare mai complicată implică un pic de algebră. Tăiați zmeul peste diagonala mai scurtă pentru a forma două triunghiuri cu diagonala mai scurtă (a) ca bază. Astfel, aria primului triunghi este a * squiggly, unde squiggly este înălțimea. Aria celui de-al doilea triunghi este a * (b – squiggly), unde (b – squiggly) este partea rămasă a diagonalei mai lungi. Aria totală devine astfel ( a * squiggly) + ( a * (b – squiggly)). Factorizând a, avem a (squiggly + b – squiggly) = ab.

Ei bine, ce știi. Practic, trebuie doar să cunoașteți formula pentru zona unui paralelogram și apoi să obțineți formula pentru celelalte.