Distribuție Poisson
Având în vedere un proces Poisson, probabilitatea de a obține exact 
succese în 
este dată de limita unei distribuții binomiale
 |
(1)
|
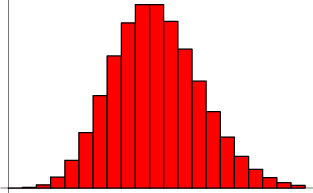
Vizualizarea distribuției în funcție de numărul așteptat de succese
 |
(2)
|
în loc de dimensiunea eșantionului 
pentru 
fix, ecuația (2) devine apoi
 |
(3)
|
Lăsând dimensiunea eșantionului 
să devină mare, distribuția se apropie apoi
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
care este cunoscută sub numele de distribuție Poisson (Papoulis 1984, pp. 101 și 554; Pfeiffer și Schum 1973, p. 200). Rețineți că dimensiunea eșantionului 
a renunțat complet la funcția de probabilitate, care are aceeași formă funcțională pentru toate valorile 
.
Distribuția Poisson este implementată în WolframLanguage ca PoissonDistribution.
Așa cum era de așteptat, distribuția Poisson este normalizată astfel încât suma probabilităților să fie egală cu 1, deoarece
 |
(9 )
|
Raportul probabilităților este dat de
 |
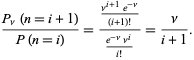(10)
|
Distribuția Poisson atinge un maxim când
 |
(11)
|
unde este constanta Euler-Mascheroni și 
este un număr armonic, care duce la ecuația transcendentală
 |
(12)
|
care nu poate fi rezolvat exact pentru 
.
Funcția generatoare de momente a distribuției Poisson este dată de
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
deci
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, p. 1). 554).
Momentele brute pot fi calculate și direct prin însumare, ceea ce produce o conexiune neașteptată cu polinomul Bell 
și numerele Stirling de al doilea fel,
 |
(21)
|
cunoscută sub numele de formula lui Dobiński.Prin urmare,
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
Momentele centrale pot fi apoi calculate ca
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
deci media, varianța, asimetria și excesul de kurtoză sunt
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
Funcția caracteristică pentru distribuția Poissond este
(Papoulis 1984, pp. 154 și 554), iar funcția generatoare de cumulant este
 |
(34)
|
deci
 |
(35)
|
Abaterea medie a distribuției Poisson este dată de
 |
(36)
|
Distribuția Poisson poate fi exprimată și în termeni de
 |
(37)
|
 |
(38)
|
Funcția generatoare de momente a distribuției aPoisson în două variabile este dată de
 |
(39)
|
Dacă variabilele independente 
, 
, …, 
au distribuții Poisson cu parametri 
, 
, …, 
, apoi
 |
(40)
|
are o distribuție Poisson cu parametru
 |
(41)
|
Acest lucru poate fi văzut deoarece funcția generatoare de cumulant este
 |
(42)
|
 |
(43)
|
Saslaw (1989) a folosit o generalizare a distribuției Poisson pentru a modela gruparea observată de galaxii în univers. Forma acestei distribuții este dată de
 |
(44)
|
unde 
este numărul de galaxii dintr-un volum 
, 
, 
este densitatea medie a galaxiilor și 
, cu 
este raportul dintre energia gravitațională și cea cinetică energie a mișcărilor deosebite, Leasing 
oferă
 |
(45)
|
care este într-adevăr o distribuție Poisson cu 
. În mod similar, lăsarea 
oferă 
.