Distribuție exponențială
de Marco Taboga, PhD
Distribuția exponențială este o distribuție continuă de probabilitate utilizată pentru modelează timpul pe care trebuie să-l așteptăm înainte de a se produce un anumit eveniment. Este contrapartida continuă a distribuției geometrice, care este în schimb discretă.
Uneori se mai numește distribuție exponențială negativă.
Introducere
Cât timp va trece înainte ca un cutremur să apară într-o anumită regiune? Cât timp trebuie să așteptăm până când un client intră în magazinul nostru? Cât va dura până când un centru de apeluri primește următorul apel telefonic? Cât timp va funcționa o piesă de mașină fără a se defecta?
Întrebări precum acestea sunt frecvent răspunse în termeni probabilistici utilizând distribuția exponențială.
Toate aceste întrebări privesc timpul de care avem nevoie să aștepte înainte de a se produce un eveniment dat. Dacă acest timp de așteptare este necunoscut, este adesea potrivit să-l considerăm ca o variabilă aleatorie având o distribuție exponențială.
Aproximativ, timpul 
de care avem nevoie a aștepta înainte ca un eveniment să aibă o distribuție exponențială dacă probabilitatea ca evenimentul să se producă într-un anumit interval de timp este proporțională cu lungimea acelui interval de timp.
Mai precis, are o distribuție exponențială dacă probabilitatea condițională este aproximativ proporțională cu lungimea a intervalului de timp cuprins între timpuri și , pentru orice moment instant .
În multe situații practice, această proprietate este foarte realistă. Acesta este motivul pentru care distribuția exponențială este atât de utilizată pentru modelarea timpilor de așteptare.
Distribuția exponențială este strict legată de distribuția Poisson. Dacă 1) un eveniment poate apărea de mai multe ori și 2) timpul scurs între două apariții succesive este distribuit exponențial și independent de aparițiile anterioare, atunci numărul de apariții al evenimentului într-o anumită unitate de timp are o distribuție Poisson. Invităm cititorul să vadă prelegerea despre distribuția Poisson pentru o explicație mai detaliată și o reprezentare grafică intuitivă a acestui fapt.
Definiție
Distribuția exponențială este caracterizată după cum urmează.
Definiție Fie o variabilă continuă aleatorie. Fie suportul său setul de numere reale pozitive: Fie . Spunem că are o distribuție exponențială cu parametrul dacă și numai dacă funcția sa de densitate de probabilitate este Parametrul se numește parametru de rată.
O variabilă aleatorie având o distribuție exponențială este numită și variabilă aleatorie exponențială.
Următoarea este o dovadă că este o funcție legitimă de densitate a probabilității.
Non-negativitatea este evidentă. Trebuie să dovedim că integralul peste este egal cu . Acest lucru este dovedit după cum urmează:
Pentru a înțelege mai bine distribuția exponențială, puteți arunca o privire asupra graficelor sale de densitate.
Parametrul ratei și interpretarea acestuia
Am menționat că probabilitatea ca evenimentul să aibă loc între două date și este proporțional cu (condiționat de informația că nu a avut loc înainte de ). Parametrul de rată este constanta proporționalității: unde este un infinitesimal de ordin mai mare decât (adică o funcție care merge la zero mai repede decât does).
Condiția de proporționalitate de mai sus este, de asemenea, suficientă pentru a caracteriza complet distribuția exponențială.
Propoziție Condiția de proporționalitate este satisfăcut numai dacă are o distribuție exponențială.
Probabilitatea condițională poate fi scrisă ca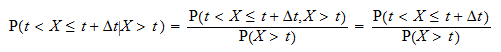 
Notați cu funcția de distribuție a , adică și prin funcția sa de supraviețuire: Apoi, Împărțirea ambelor părți la , obținem unde este o cantitate care tinde să când tinde să . Luând limite de ambele părți, obținem sau, prin definiția derivatei: Această ecuație diferențială este ușor de rezolvat folosind lanțul regula: Luând integralul de la la de ambele părți, obținem și sau Dar (deoarece nu poate lua valori negative) implică Exponențierea ambelor părți, obținem Prin urmare, sau Dar funcția de densitate este prima derivată a funcției de distribuție: iar termenul cel mai drept este densitatea unei variabile aleatorii exponențiale. Prin urmare, condiția de proporționalitate este îndeplinită numai dacă este o variabilă exponențială aleatorie
Valoarea așteptată
Valoarea așteptată a unei variabile aleatorii exponențiale este
Poate fi derivat după cum urmează: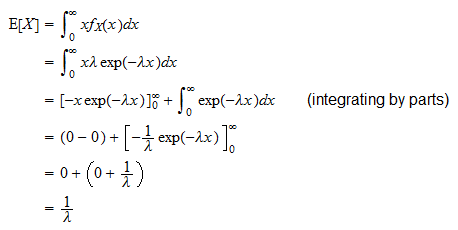 
Varianță
Varianța unui variabila exponențială aleatorie este
It poate fi derivat datorită formulei obișnuite de varianță (): 
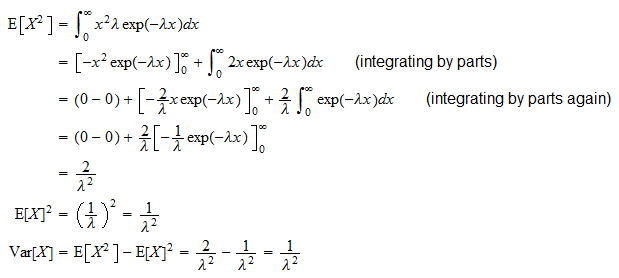
Funcția de generare a momentului
Funcția de generare a momentului unei variabile aleatorii exponențiale este definită pentru orice :
Definiția funcției de generare a momentului dă De desigur, integralele de mai sus converg numai dacă , adică numai dacă . Prin urmare, funcția generatoare de moment a unei variabile exponențiale aleatorii există pentru toate .
Funcția caracteristică
Funcția caracteristică a unei variabile aleatorii exponențiale este
Utilizând definiția funcției caracteristice și faptul că putem scrie Acum calculăm separat cele două integrale . Prima integrală este 
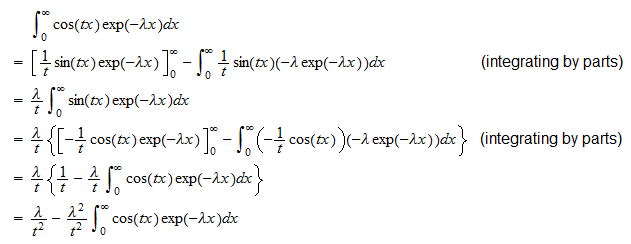Prin urmare, care poate fi rearanjat pentru a produce sau A doua integrală este 
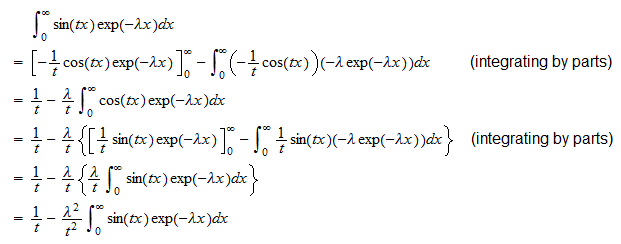Prin urmare, care poate fi rearanjat pentru a produce sau Punând bucăți împreună, obținem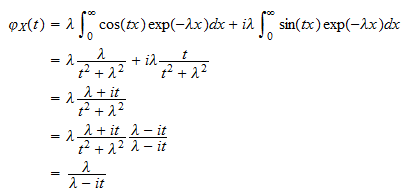 
Funcția de distribuție
Funcția de distribuție a unei variabile aleatorii exponențiale este
Dacă , atunci deoarece nu poate lua valori negative. Dacă , atunci
Mai multe detalii
În următoarele subsecțiuni puteți găsi mai multe detalii despre distribuția exponențială.
Proprietatea fără memorie
Una dintre cele mai importante proprietăți ale distribuției exponențiale este proprietatea fără memorie: pentru orice .
Acest lucru este dovedit după cum urmează: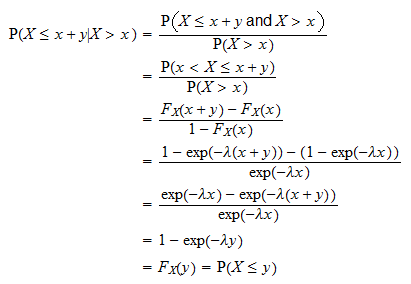 
este timpul pe care trebuie să-l așteptăm înainte de un anumit eveniment apare. Proprietatea de mai sus spune că probabilitatea ca evenimentul să aibă loc într-un interval de timp este independentă de cât timp a trecut deja () fără ca evenimentul să se întâmple.
Suma variabilelor aleatorii exponențiale este o variabilă aleatorie Gamma
Să presupunem , , …, sunt variabile aleatorii independente reciproc, având distribuție exponențială cu parametrul .
Definiți
Apoi, suma este o variabilă aleatorie Gamma cu parametri și .
Acest lucru este dovedit folosind moment funcții de generare (amintiți-vă că funcția de generare a momentului unei sume de variabile aleatorii reciproc independente este doar produsul funcțiilor lor de generare a momentului): Acesta din urmă este funcția generatoare de moment a unei game distribuție cu parametrii și . Deci, are o distribuție Gamma, deoarece două variabile aleatorii au aceeași distribuție atunci când au aceeași funcție de generare a momentului.
Variabila aleatorie se spune uneori că are o distribuție Erlang. Distribuția Erlang este doar un caz special al distribuției Gamma: o variabilă aleatorie Gamma este, de asemenea, o variabilă aleatorie Erlang atunci când poate fi scrisă ca o sumă de variabile aleatorii exponențiale.
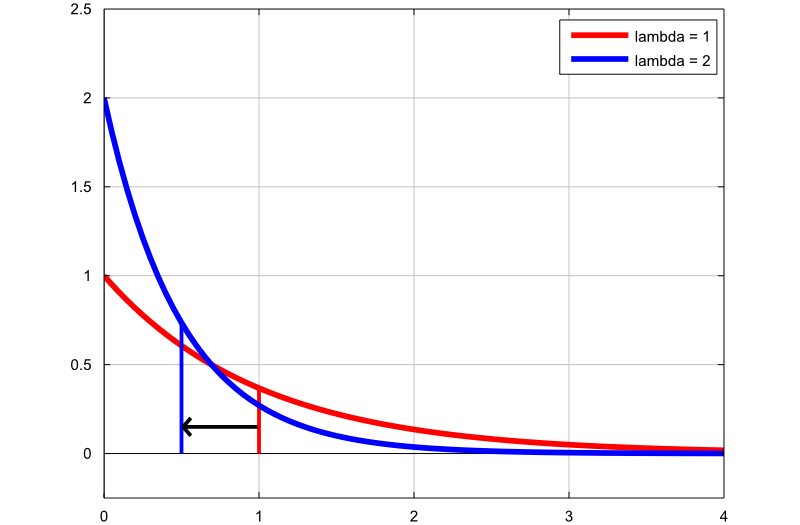
Grafic de densitate
p> Următorul grafic arată cum se modifică densitatea distribuției exponențiale prin schimbarea parametrului de rată:
-
primul grafic (linia roșie) este funcția densității probabilității unei variabile aleatorii exponențiale cu parametrul ratei
; -
al doilea grafic (linia albastră) este funcția de densitate a probabilității unei variabile aleatorii exponențiale cu parametrul de rată
.
Liniile verticale subțiri indică mijloacele celor două distribuții. Rețineți că, prin creșterea parametrului de rată, reducem media distribuției de la la .
Exerciții rezolvate
Mai jos puteți găsi câteva exerciții cu soluții explicate.
Exercițiul 1
Fie o variabilă exponențială aleatorie cu parametrul . Calculați următoarea probabilitate:
În primul rând putem scrie probabilitatea ca folosind faptul că probabilitatea ca o variabilă continuă aleatorie să ia orice valoare specifică este egală cu zero (vezi Variabile aleatoare continue și evenimente de probabilitate zero). Acum, probabilitatea poate fi scrisă în funcție de funcția de distribuție a ca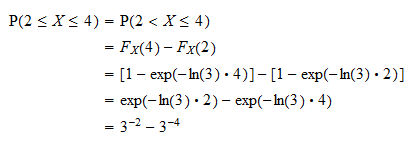 
Exercițiul 2
Să presupunem că variabila aleatorie are o distribuție exponențială cu parametrul . Calculați următoarea probabilitate:
Această probabilitate poate fi calculată cu ușurință utilizând funcția de distribuție a :
Exercițiul 3
Care este probabilitatea ca o variabilă aleatorie este mai mic decât valoarea sa așteptată, dacă are o distribuție exponențială cu parametrul ?
Valoarea așteptată a unei variabile aleatorii exponențiale cu parametrul este Probabilitatea de mai sus poate fi calculată utilizând funcția de distribuție a :
Cum se citează
Vă rugăm să citați ca: