Cum se calculează volumul

Calculul volumului

Volumul se măsoară în cuburi (sau unități cubice).

Câte cuburi sunt în această prismă dreptunghiulară (cuboidă)?

Putem număra cuburile, deși este mai rapid să iei lungimea, lățimea și înălțimea și să folosești înmulțirea. Prisma dreptunghiulară de mai sus are un volum de 48 de unități cubice.

Volumul unei prisme dreptunghiulare este = lungime x lățime x înălțime

Exemple de calcul al ariei unui dreptunghi

Trebuie să facem două înmulțiri pentru a calcula volumul. Calculăm aria unei fețe (sau laterale) și o înmulțim cu înălțimea sa. Exemplele de mai jos arată cum există trei moduri de a face acest lucru.

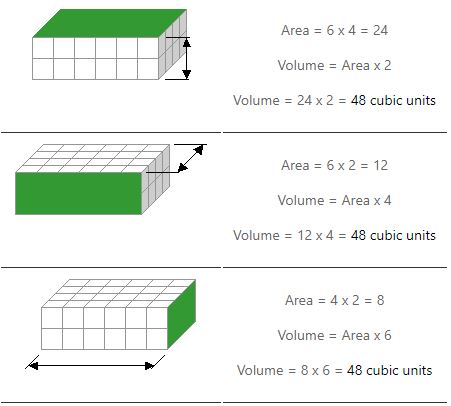
Observați cum obținem același răspuns indiferent de ce parte folosim pentru a găsi o zonă.

Când copilul dvs. începe să lucreze cu zona și perimetrul, el sau ea va lucra de obicei cu 2 dimensiuni – pătrate, dreptunghiuri, triunghiuri etc. care sunt afișate pe hârtie ca plate – nu există adâncime sau a treia dimensiune. Lucrul cu volum implică 3 dimensiuni. Asigurați-vă că copilul dvs. este conștient de acest lucru și nu se gândește la cuburi și la alte forme 3D afișate pe hârtie ca fiind doar o altă „formă pe pagină”. Arătați-le cutii reale și arătați cum pot fi desenate (sau reprezentate) pe o bucată de hârtie bidimensională. Cu alte cuvinte, asigurați-vă că există o legătură între ceea ce este pe hârtie și ceea ce reprezintă în lumea reală.

Asigurați-vă că copilul dvs. nu este confuz de utilizarea volumului așa cum este folosit atunci când vorbiți despre sonoritate .

Unități pentru măsurarea volumului

Există diferențe foarte mari între unitățile de măsură pentru volum. De exemplu, există 100 de centimetri într-un metru, dar există 1.000.000 (da, 1 milion ) centimetri cubi într-un metru cub.

De ce marea diferență? Pentru că în volum nu avem doar lungimea; avem lungimea, lățimea și înălțimea. Exemplul de cub de zahăr de mai jos arată acest lucru.

Cât zahăr? 1 m3 sau 1.000.000 cm3

Gândiți-vă să umpleți o cutie foarte mare (ar avea 1 metru lățime, 1 metru, lungime și un metru înălțime) cu cuburi de zahăr (cu fiecare lat 1 centimetru).

	Pasul 1: un rând de-a lungul fundului casetei – care ar fi 100 cuburi de zahăr
	Pasul 2: acoperiți restul bazei cutiei – care ar da un total de 100 de rânduri fiecare cu 100 de cuburi de zahăr. 100 x 100 = 10.000 cuburi de zahăr în partea de jos a cutiei mari.
	Pasul 3: Repetați acest lucru de 99 de ori până când există straturi de 10.000 de cuburi stivuite la 100 de adâncimi. 10.000 x 100 = 1.000.000 de cuburi de zahăr

Există 1.000.000 cm3 în 1 m3 – aveți grijă să nu aveți prea mult zahăr!

Există alte unități pentru măsurarea volumului; centimetri cubi, picioare cubice, metri cubi sunt toate unitățile utilizate pentru măsurarea volumului. Mililitri, litri, galoane sunt, de asemenea, folosite mai ales la măsurarea lichidelor.

Nu uitați de wee 3

Scriem dimensiuni cubice folosind un mic 3 lângă unitate.
Scriem mm3, cm3, m3, km3, cm3
Putem spune „85 centimetri cubici” sau „85 centimetri cubi”

Exemple de calcul al volumului de prisme dreptunghiulare

	Volum = Lungime x Lățime x Înălțime Volum = 12 cm x 8 cm x 6 cm = 576 cm3
	Volum = Lungime x Lățime x Înălțime Volum = 20 mx 2 mx 2 m = 80 m3
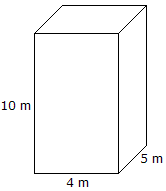	Volum = Lungime x Lățime x Înălțime Volum = 10 mx 4 mx 5 m = 200 m3

Volumul unui cilindru

Calculul volumului unui cilindru der implică multiplicarea suprafeței bazei cu înălțimea cilindrului. Baza unui cilindru este circulară și formula pentru aria unui cerc este: aria unui cerc = πr2. Există mai multe aici în zona unui cerc.

Volum = Suprafața bazei x Înălțime Volum = πr2 xh Volum = πr2 h

Notă: în exemplele de mai jos vom folosi 3.14 ca valoare aproximativă pentru π (Pi).

Exemplu de calcul al volumului unui cilindru

Dimensiunile sunt în cm.

Volum = πr2 h Volum = 3.14 x 3 x 3 x 8 Volum = 226,08 cm3

Volumul unui con

Volumul unui con este egal cu o treime din volumul unui cilindru cu înălțimea și aria de bază potrivite. Aceasta oferă formula pentru volumul unui con așa cum se arată mai jos.

Volum = 1/3 πr2h

Exemplu de calcul al volumului unui con

Dimensiunile sunt în cm.

Volum = 1/3 πr2 h Volum = 1/3 x 3,14 x 2 x 2 x 7 Volum = 29,31 cm3

Volumul unei sfere

Formula pentru volumul unei sfere este prezentată mai jos.

Volume = 4/3 πr3

Exemplu de calcul al volumului unei sfere

Dimensiunile sunt în cm.

Volum = 4/3 πr3 Volum = 4/3 x 3,14 x 4 x 4 x 4 Volum = 267,95 cm3

Fișe de lucru cu volum imprimabil

Utilizați foaia de lucru de mai jos pentru a practica calculul volumelor.

• Găsirea volumului în unități cubice – prisme dreptunghiulare compozite
• Volumele prismelor dreptunghiulare
• Volumele prismelor dreptunghiulare
• Volumele obiectelor „din lumea reală” de ex. de cutii de cereale
• Calculul volumelor de ex. a prismelor și cilindrilor triunghiulari

Aici veți primi alte foi de geometrie pe perimetru, suprafață și multe altele.