Cum se calculează suprafața
Suprafața de calcul
Suprafața este măsurată în pătrate (sau unități pătrate).
Câte pătrate sunt în acest dreptunghi?

Putem număra pătratele sau putem ia lungimea și lățimea și folosește înmulțirea. Dreptunghiul de mai sus are o suprafață de 15 unități pătrate.
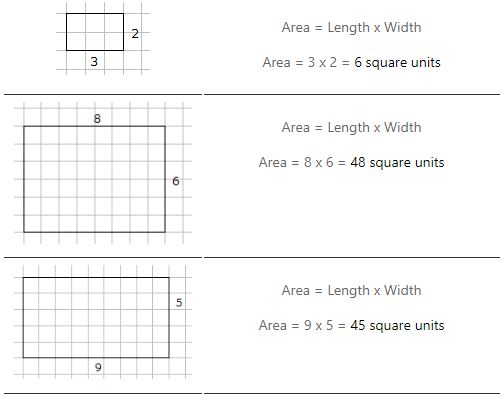
Aria unui dreptunghi este = lungime x lățime
Exemple de calcul al ariei unui dreptunghi
Unități pentru zona de măsurare
Măsurăm zona folosind pătrate. Folosim diferite dimensiuni de pătrate în funcție de cât de mare sau mică este o zonă.
| Exemplu | Lungimea laturii pe pătrate | Unitate |
| Dimensiunea cuie pe degetul mare | Milimetru | mm2 |
| Dimensiunea bucății de hârtie | Centimetru | cm2 |
| Dimensiunea unei camere | Contor | m2 |
| Dimensiunea unui oraș | Kilometru | km2 |
Nu uitați de wee 2
Scriem dimensiuni pătrate folosind un mic 2 lângă unitate.
Scriem mm2, cm2, m2, km2, cm2
Putem spune „63 milimetri pătrat” sau „63 milimetri pătrat”
Am putea folosi pătrate mici pentru a măsura suprafețe mari. Singura problemă cu aceasta este că vom ajunge să folosim foarte mari numere. De exemplu, un câmp ar putea fi măsurat la 5.000.000.000 de milimetri pătrați atunci când 5.000 de metri pătrați ar fi o dimensiune mult mai ușor de spus, scris și vizualizat.
Probabil veți auzi mai multe unități pentru suprafața de măsurare; centimetri pătrați, metri pătrați, metri pătrați, mile pătrate, acri, hectare sunt toate unități utilizate pentru măsurarea suprafeței.
Mai multe exemple de suprafață de calcul
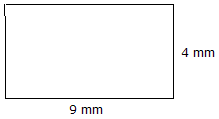 |
Suprafață = lungime x lățime suprafață = 9 mm x 4 mm = 36 mm2 |
 |
Suprafață = lungime x lățime suprafață = 7 cm x 6 cm = 42 cm2 |
 |
Suprafață = Lungime x Lățime Suprafață = 8 mx 2 m = 16 m2 |
 |
Suprafață = Lungime x Lățime Suprafață = 7 km x 5 km = 35 km2 |
Zona unui pătrat
Lungimea și lățimea unui pătrat sunt aceleași, deci trebuie doar să înmulțim lungimea cu lungimea.
| Suprafață = lungime x lungime suprafață = 6 cm x 6 cm = 36 cm2 |
Aria unui cerc
Aria unui cerc = πr2
unde r este raza cercului și π este raportul dintre circumferința unui cerc și diametrul său.
π (pronunțat „plăcintă” și adesea scris „Pi”) este o zecimală infinită cu o comună aproximativ de 3,14159. Puteți afla mai multe despre Pi aici
Exemplu de calcul al ariei unui cerc
 |
Area = πr2 Area = 3.14159 x (4 cm) 2 Suprafață = 3,14159 x 16 cm2 Suprafață = 50,27 cm2 Răspuns rotunjit la 2 zecimale |
Explicația zonei unei formule de cerc
Luați un cerc și împărțiți-l în sectoare de dimensiuni egale și rearanjați-le așa cum se arată mai jos. Observați cum, pe măsură ce sectoarele devin mai mici, forma devine mai mult ca un dreptunghi. Notă: Nu există nicio limită pentru cât de mici ar putea fi aceste sectoare și pentru cât de aproape ar putea semăna cu un dreptunghi atunci când sunt aranjate.
Presupunând că știm că circumferința unui cerc este egală cu 2πr, putem adăuga dimensiuni la „dreptunghiul” așa cum se arată mai jos. Folosind aria unei formule a ariei dreptunghiului, aria = lățimea x înălțimea putem vedea cum se poate arăta că cercul nostru, reconfigurat ca dreptunghi, are o zonă care se apropie de πr xr sau πr2
Cerc Sectoare rearanjate

Sectoare cercuri rearanjate – Pornire a arăta ca un dreptunghi

Forme compuse
Există multe cazuri în care calculul unei suprafețe totale necesită mai mult de o suprafață care urmează să fie calculată, urmată fie de o adunare, scădere sau de o altă combinație de operații pentru a găsi aria necesară.
Notă: în exemplele de mai jos nu sunt afișate unitățile de măsură și răspunsurile și valoarea π (Pi) au fost rotunjite la cea mai apropiată sutime.
Exemplu: Forme simple compuse
Exemplul de calcul al suprafeței de mai jos este relativ simplu. Forma poate fi văzută ca un triunghi combinat cu un dreptunghi.
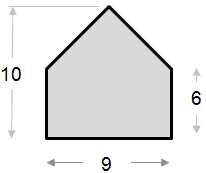 |
Zona părții triunghiului: ½ x bază x înălțime ½ x 9 x 4 = 18 Suprafața dreptunghiului: Suprafață totală = 18 + 54 = 72 |
Exemplul de mai sus ilustrează o cerință comună atunci când se lucrează cu compus forme – găsirea dimensiunilor care nu sunt afișate. Când vă îndrumați copiii, acordați ajutor, atunci când este necesar, pentru a găsi aceste dimensiuni „lipsă”. Există un alt exemplu mai jos.
Găsirea dimensiunilor
 |
Care sunt dimensiunile părții mici dreptunghiulare? Lățime? 12 – 7 – 2 = 3 Înălțime? 8 – 6 = 2 |
Exemplu: scăderea unei zone din alta
În exemplul de mai jos, forma poate fi văzută ca un dreptunghi cu un triunghi decupat.
 |
Aria părții dreptunghiului: lățime x înălțime 5 x 6 = 30 Aria părții triunghiului: Suprafața totală = 30 – 4,50 = 25,50 |
Exemplu: zone parțiale
Exemplul de mai jos este similar cu unul de mai sus, deși avem un semicerc, trebuie să calculăm o fracție (o jumătate) a zonei cercului. Rețineți în acest exemplu diametrul și nu raza este afișat.
 |
Aria părții triunghiului: ½ x baza x înălțimea ½ x 6 x 6 = 18 Aria părții semicercului: Suprafața totală = 18 – 3,53 = 14,47 |
Exemplu: Decizii! Combina? Scădere
Este obișnuit să aveți mai multe modalități de a calcula aria finală. În exemplele de mai jos, forma poate fi văzută ca două dreptunghiuri combinate sau ca un dreptunghi mare cu un dreptunghi mai mic „decupat” din colțul din dreapta sus.
Calcularea foilor de lucru cu suprafața
Tipărire extrageți foile de lucru enumerate mai jos și folosiți-le pentru a vă exersa copiii.
- Calculul zonelor – dreptunghiuri și pătrate
- Calcularea zonelor – dreptunghiuri
- Calculul Zonele – dreptunghiuri
- Calculul zonelor compuse, de ex cu forme dreptunghiulare
- Calculul ariilor compuse de ex. cu dreptunghiuri, triunghiuri și cercuri
- Zone de calcul, de ex. a triunghiurilor
- Suprafața unui cerc
- Calculul suprafețelor de ex. de prisme dreptunghiulare
Aici veți găsi mai multe foi de lucru cu geometrie imprimabile.