College Algebra (Română)
Rezultatele învățării
- Identificați vârful, axa de simetrie, interceptarea y și valoarea minimă sau maximă a unei parabole din este graficul.
- Identificați o funcție pătratică scrisă în general și sub formă de vârf.
- Având în vedere o funcție pătratică în formă generală, găsiți vârful.
- Definiți domeniul și gama unei funcții pătratice prin identificarea vârfului ca maxim sau minim.
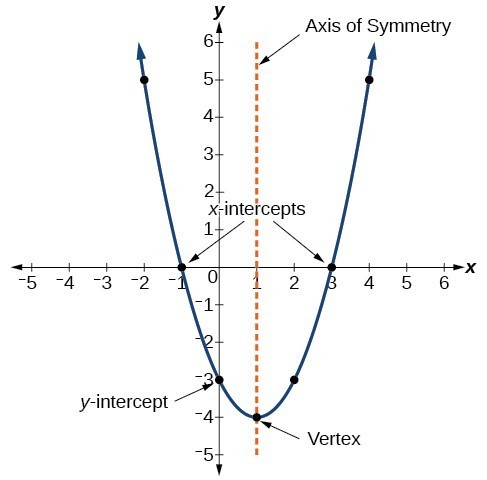
Graficul unei funcții pătratice este o curbă în formă de U numită parabolă. O caracteristică importantă a graficului este că are un punct extrem, numit vârf. Dacă parabola se deschide, vârful reprezintă cel mai mic punct de pe grafic sau valoarea minimă a funcției pătratice. Dacă parabola se deschide, vârful reprezintă cel mai înalt punct de pe grafic sau valoarea maximă. În ambele cazuri, vârful este un punct de cotitură pe grafic. Graficul este, de asemenea, simetric cu o linie verticală trasată prin vârf, numită axa de simetrie.
Ecuații ale funcțiilor quadratice
Forma generală a unei funcții pătratice prezintă funcția în forma
f \ left (x \ right) = a {x} ^ {2} + bx + c
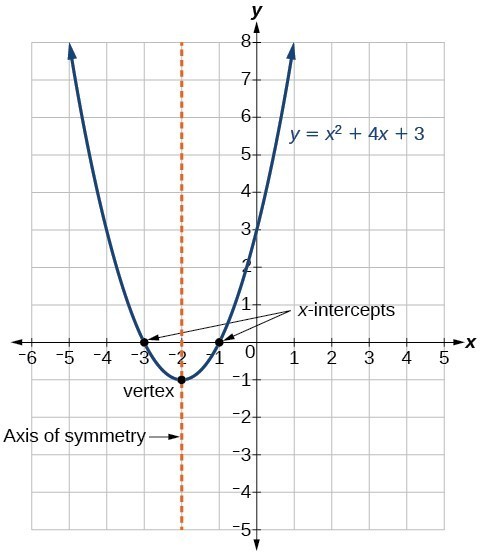
Forma standard a unei funcții pătratice prezintă funcția în forma
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Având o funcție pătratică în general forma, găsiți vârful parabolei.
Un motiv pentru care am putea dori să identificăm vârful parabolei este că acest punct ne va informa unde apare valoarea maximă sau minimă a ieșirii, k și unde apare, h. Dacă ni se dă forma generală a unei funcții pătratice:
f (x) = ax ^ 2 + bx + c
Putem defini vârful, (h, k), procedând în felul următor:
Găsirea domeniului și intervalului unei funcții quadratice
Orice număr poate fi valoarea de intrare a unei funcții pătratice. Prin urmare, domeniul oricărei funcții pătratice este toate numerele reale. Deoarece parabolele au un maxim sau un minim la vârf, intervalul este restricționat. Deoarece vârful unei parabole va fi fie maxim sau minim, intervalul va consta din toate valorile y mai mari sau egale cu coordonata y a vârfului sau mai mici sau egale cu coordonata y la punctul de cotitură , în funcție de parabola care se deschide sau se deschide.
Contribuie!
Îmbunătățiți această paginăAflați mai multe