Identificați asimptotele verticale și orizontale | College Algebra

noiembrie 8, 2020

College Algebra (Română)

Privind graficul unei funcții raționale, putem investiga comportamentul său local și putem vedea cu ușurință dacă există asimptote. Este posibil să putem chiar să aproximăm locația lor. Chiar și fără grafic, totuși, putem determina dacă o anumită funcție rațională are asimptote și să calculăm locația lor.

Asimptote verticale

Asimptotele verticale ale unei funcții raționale pot fi constatate prin examinarea factorilor numitorului care nu sunt comuni factorilor din numărător. Asimptotele verticale apar la zerourile unor astfel de factori.

Cum să: Având o funcție rațională, identificați orice asimptote verticale ale graficului său.

Factorizați numeratorul și numitor.
Rețineți orice restricții din domeniul funcției.
Reduceți expresia anulând factorii comuni din numerator și numitor.
Rețineți orice valori care fac ca numitorul să fie zero în această versiune simplificată. Aici apar asimptotele verticale.
Rețineți orice restricții din domeniul în care nu apar asimptotele. Acestea sunt discontinuități amovibile.

Discontinuități amovibile

Ocazional, un grafic va conține o gaură: un singur punct în care graficul nu este definit, indicat de un cerc deschis. O astfel de gaură o numim discontinuitate amovibilă.

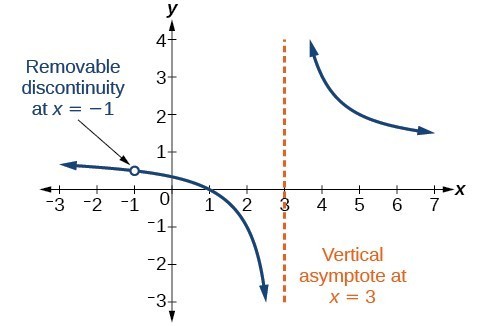
f \ left (x \ right) = \ frac {\ left (x + 1 \ right) \ left (x – 1 \ right)} {\ left (x + 1 \ right) \ left (x – 3 \ right)}

Figura 10

O Notă generală: discontinuități amovibile ale funcțiilor raționale

O discontinuitate amovibilă apare în graficul unei funcții raționale la x = a dacă a este zero pentru un factor din numitor care este comun cu un factor din numărător. Factorizăm numeratorul și numitorul și verificăm factorii comuni. Dacă găsim vreunul, stabilim factorul comun egal cu 0 și rezolvăm. Aceasta este locația discontinuității amovibile. Acest lucru este adevărat dacă multiplicitatea acestui factor este mai mare sau egală cu cea din numitor. Dacă multiplicitatea acestui factor este mai mare în numitor, atunci există încă o asimptotă la acea valoare.

Asimptotele orizontale

În timp ce asimptotele verticale descriu comportamentul unei grafic pe măsură ce ieșirea devine foarte mare sau foarte mică, asimptotele orizontale ajută la descrierea comportamentului unui grafic pe măsură ce intrarea devine foarte mare sau foarte mică. Amintiți-vă că comportamentul final al unui polinom îl va reflecta pe cel al termenului principal. În mod similar, comportamentul final al unei funcții raționale va reflecta raportul dintre termenii principali ai funcțiilor numărătorului și numitorului.

Există trei rezultate distincte atunci când se verifică asimptotele orizontale:

Caz 1: Dacă gradul numitorului > gradul numărătorului, există o asimptotă orizontală la y = 0.

\ text {Exemplu:} f \ left (x \ right) = \ frac {4x + 2} {{x} ^ {2} + 4x – 5}

Cazul 2: Dacă gradul numitorului < gradul numărătorului cu unul, vom obține o asimptotă înclinată.

\ text {Exemplu:} f \ left (x \ right) = \ frac {3 {x} ^ {2} -2x + 1} {x – 1}

\ text {Exemplu:} f \ left (x \ right) = \ frac {3 {x} ^ {2} +2} {{x} ^ {2 } + 4x – 5}

Observați că, în timp ce graficul unei funcții raționale nu va traversa niciodată o asimptotă verticală, graficul poate sau nu să traverseze o orizontală sau asimptotă înclinată. De asemenea, deși graficul unei funcții raționale poate avea multe asimptote verticale, graficul va avea cel mult o asimptotă orizontală (sau înclinată).

Trebuie remarcat faptul că, dacă gradul numărătorului este mai mare decât gradul numitorului de mai mult de unul, comportamentul final al graficului va imita comportamentul fracției de comportament final redus. De exemplu, dacă am avea funcția

f \ left (x \ right) = \ frac {3 {x} ^ {5} – {x} ^ { 2}} {x + 3}

cu comportament final

f \ left (x \ right) \ approx \ frac {3 {x } ^ {5}} {x} = 3 {x} ^ {4},

comportamentul final al graficului ar arăta similar cu cel al unui polinom uniform cu un coeficient pozitiv de conducere.

x \ to \ pm \ infty, f \ left (x \ right) \ to \ infty

O Notă generală: Asimptote orizontale ale Funcții raționale

Asimptota orizontală a unei funcții raționale poate fi determinată examinând gradele numărătorului și numitorului.

Gradul numărătorului este mai mic decât gradul numitorului: asimptotă orizontală la y = 0.
Gradul numărătorului este mai mare decât gradul numitorului cu unul: nu există asimptotă orizontală; asimptotă înclinată.
Gradul numărătorului este egal cu gradul numitorului: asimptotă orizontală la raportul dintre coeficienții de conducere.

O Notă generală: interceptări ale funcțiilor raționale

O funcție rațională va avea o interceptare y când intrarea este zero, dacă funcția este definită la zero. O funcție rațională nu va avea o interceptare y dacă funcția nu este definită la zero.

La fel, o funcție rațională va avea interceptări x la intrări care determină ieșirea să fie zero. Deoarece o fracțiune este egală cu zero doar când numeratorul este zero, interceptările x pot apărea numai atunci când numeratorul funcției raționale este egal cu zero.

Încercați-l 7

Având în vedere funcția pătrată reciprocă care este deplasată la dreapta cu 3 unități și în jos cu 4 unități, scrieți aceasta ca o funcție rațională. Apoi, găsiți interceptările x– și y și asimptotele orizontale și verticale.

Soluție

admin