Medição: Descobrindo fórmulas para área

Fórmulas de área

Alunos que têm a noção informal de que a área é a “quantidade de 2-D coisas “” contidas dentro de uma região podem inventar por si mesmos a maioria das fórmulas que muitas vezes são solicitados apenas a memorizar. Cada fórmula que reinventam ajuda a fortalecer sua compreensão (e memória) das outras fórmulas que conhecem. (Veja também área de superfície.)

Área dos retângulos

Ao escolher um quadrado como unidade de área, temos uma ideia intuitiva sobre a área dos retângulos. Se decidirmos que a área deste quadrado é 1, então um retângulo que é 7 vezes mais longo teria 7 × 1 como sua área.

Um retângulo com o dobro da altura de teria o dobro de sua área, então a área de é 2 × 7 unidades de área. Podemos contar as duas linhas de sete quadrados. Da mesma forma, tem 3 linhas de 7 quadrados (ou 7 colunas de 3 quadrados), para um total de 7 × 3 quadrados, então sua área é de 21 unidades quadradas.

O número de quadrados em uma linha é o comprimento do retângulo. O número de linhas é a altura do retângulo. Portanto, a área é comprimento × altura.

Como um retângulo pode ser desenhado em uma inclinação, “altura” é definida como “a direção perpendicular à base” e “base” é definida como, bem, seja qual for o lado que você escolher.

Isso funciona para contar números. Funciona até mesmo para frações. 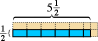O retângulo azul mostrado aqui mede a metade unidade de comprimento de altura por cinco unidades e meio de comprimento de largura. Se escolhermos o quadrado correspondente como nossa unidade de área, veremos que o retângulo azul contém cinco unidades de meia área e um quarto de unidade de área, ou um total de unidades de dois e três quartos de área. (As partes rosa mostram a conclusão de cada unidade de área quadrada.)

Para incluir todos os números, definimos a área de um retângulo como base × altura (onde “base” e “altura” significam os comprimentos desses lados, medidos nas mesmas unidades).

Área dos paralelogramos

Obtendo a ideia

Podemos descobrir uma fórmula para a área de um paralelogramo por dissecação ajustando o paralelogramo e reorganizando as partes para fazer um retângulo. Como o paralelogramo e o retângulo são compostos das mesmas partes, eles necessariamente têm a mesma área. (Veja a definição de área para mais informações sobre por que essas áreas são iguais.)

Podemos ver que eles também têm exatamente o mesmo comprimento da base (azul) e exatamente a mesma altura (verde). Como base × altura fornece a área do retângulo, podemos usar as mesmas medidas no paralelogramo para calcular sua área: base × altura. (Como antes, “altura” é medida perpendicularmente à base e “base” é o lado que você escolheu primeiro. Veja paralelogramo.)

O corte mostrado acima torna fácil ver que o comprimento da base é inalterado. Na verdade, o corte perpendicular pode ser feito em qualquer lugar ao longo da base.

Aumentando os orifícios

Intuição e prova

Esta dissecação fornece uma compreensão intuitiva da fórmula da área para um paralelogramo, uma razão pela qual deveria ser o que é. Mas não questionamos se a dissecção realmente “funciona”. Ou seja, quando cortamos o paralelogramo e reorganizamos suas partes, esperamos obter e o resultado certamente se parece com isso. as aparências enganam. O que nos garante que, quando movemos esse triângulo, o resultado é um retângulo? E se for mais parecido com (embora menos exagerado)? Se o resultado não for sempre um retângulo perfeito, não podemos usar nosso conhecimento da fórmula da área do retângulo para desenvolver uma fórmula para o paralelogramo. No ensino médio, os alunos serão capazes de provar que as duas partes do paralelogramo, quando remontadas corretamente, formam um retângulo . Nas séries K-8, na maior parte, os alunos devem confiar no experimento visual e ter uma sensação intuitiva. Saiba mais sobre por que essas dissecações funcionam.

E se escolhermos o lado menor para ser a base?

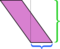
Somos livres para escolher qualquer lado como base; “altura” está definido para ser medida perpendicularmente ao lado que escolhemos como base. Se tomarmos o lado curto (azul) como base, a dissecção mostrada acima não é tão convincente. Cortar ao longo dessa altitude e reorganizar as partes deixa uma bagunça:

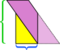
Neste exemplo específico, podemos salvar a bagunça fazendo mais um corte, 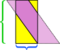mas e se o paralelogramo fosse ainda mais longo e estreito?

Acontece que qualquer paralelogramo, não importa quão longo e estreito, pode ser dissecado dessa maneira, de forma que as partes – talvez muitas delas – possam ser reorganizadas em um retângulo. Mas é preciso mais trabalho para mostrar que isso sempre pode ser feito. Precisamos de outra ideia.

Uma ideia de dissecação ligeiramente diferente torna a vida muito mais fácil neste caso. (Por conta própria, você pode mostrar que funciona no caso original também.)

• Coloque o paralelogramo em um retângulo.
• As duas partes do retângulo que não estão dentro do paralelogramo são triângulos congruentes.
• Deslize um desses triângulos em direção ao outro até que se encontrem para formar um retângulo. 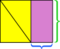Como a área total do retângulo externo não mudou (é o mesmo retângulo de antes) e a área amarela não mudou (as peças acabaram de se mover), a diferença entre eles – as áreas roxas – devem ser iguais. Como antes, também podemos ver que as dimensões da área roxa retangular são a base e a altura do paralelogramo original.

Intuição e prova, repetição : Mais uma vez, a dissecção fornece o insight essencial, mas é preciso um pouco mais de trabalho para garantir que os dois triângulos amarelos, que certamente parecem se encaixar para formar um retângulo, realmente se encaixem com precisão, e não apenas quase.

Por que é importante ter tanto cuidado?

Quando construímos outras fórmulas de área (abaixo), queremos usar nosso método de como encontrar a área de um paralelogramo, e por isso queremos para poder confiar na regra que encontramos. Podemos ter certeza de que reorganizar as partes não muda a área: é, afinal, como definimos a área. Mas também devemos ter certeza de que as peças se encaixam da maneira que afirmamos que se encaixam, ou não podemos confiar nas medições que fizemos. E devemos ter certeza de que a regra de base × altura não depende de uma escolha feliz da base.

Na maioria dos currículos, os alunos não têm uma base sistemática de conhecimento geométrico antes da 8ª série para fazer provas sólidas de que essas dissecções funcionam. Mas o entendimento intuitivo é suficiente para explicar e justificar as fórmulas, e uma boa base para estudos geométricos posteriores.

Área do triângulo

Saber como encontrar a área de um paralelogramo nos ajuda encontre a área de um triângulo.

Dissecando o triângulo

Podemos dissecar o triângulo em duas partes – uma delas um triângulo e uma delas um trapézio – cortando-o paralelamente para a base. Se cortarmos a altura exatamente pela metade com essa fatia, as duas partes se encaixam para fazer um paralelogramo com a mesma base, mas com metade da altura.

Portanto, base × meia altura fornece a área do triângulo. Uma dissecção semelhante mostra meia-base × altura. Qualquer um deles se reduz a bh.

Dobrando o triângulo e depois reduzindo à metade a área resultante

Outra maneira de pensar: duas cópias de o triângulo faz um paralelogramo com a mesma base e mesma altura do triângulo.

A área do paralelogramo é base × altura, mas isso é o dobro da área do triângulo, então a área do triângulo é de base × altura, como vimos com o método de dissecção.

(Como sempre , escolha uma “base” e meça a altura perpendicular a essa base, da base ao vértice oposto.)

Área do trapézio

Dobrando o trapézio e reduzindo pela metade a área resultante

Como acontecia com o triângulo, duas cópias de um trapézio podem ser encaixadas para formar um paralelogramo.

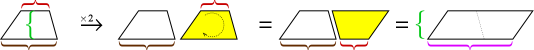
A altura do paralelogramo é igual à altura do trapézio, mas sua base é a soma das duas bases do trapézio. Portanto, a área do paralelogramo é altura × (base1 + base2). Mas essa área tem dois trapézios, então precisamos cortá-la ao meio para obter a área do trapézio.

Dissecando o trapézio

Também poderíamos dissecar o trapézio da mesma forma que dissecamos o triângulo, com uma única fatia cortando sua altura pela metade. As duas partes se encaixam para formar um paralelogramo cuja base é a soma das duas bases do trapézio, mas cuja altura é a metade da altura do trapézio.

No caso do trapézio, as bases não podem ser escolhido à vontade. Os dois lados paralelos são as bases, e a altura, como sempre, é a distância perpendicular de uma base à oposta.

A área deste paralelogramo é sua altura (meia altura do trapézio) vezes sua base (soma das bases do trapézio), então sua área é meia altura × (base1 + base2). Como o paralelogramo é feito exatamente do mesmo “material” que o trapézio, essa é a área do trapézio também.

De qualquer forma, a área do trapézio é × altura × (base1 + base2).

Área de outros quadriláteros especiais

Área do losango

A área de um losango pode ser encontrada cortando e reorganizando as peças para formar um paralelogramo. Isso pode ser feito de várias maneiras:

1. Corte na diagonal mais curta (a) para formar dois triângulos congruentes. Mova a metade inferior do triângulo para perto da metade superior para formar um paralelogramo. A diagonal mais curta (a) se torna a base do paralelogramo e a metade da diagonal mais longa (b) se torna a altura do paralelogramo. Assim, a área do losango é a * b ou o produto das diagonais, que é a fórmula padrão do losango.
2. Outra maneira semelhante é cortar o losango em quatro triângulos congruentes e reorganizá-los em um retângulo com a diagonal mais curta como base e metade da diagonal mais longa como altura.
3. Após o corte o losango em dois triângulos congruentes, podemos calcular a área de um do triângulo, que é * base (a) * altura ( b) = ab. Em seguida, multiplique por dois, pois há dois deles: 2 * ab = ab.

Área da pipa

A área de uma pipa pode ser considerada semelhante à área de um losango. Cortar a diagonal mais longa produz dois triângulos congruentes. Se as reorganizarmos, podemos formar um paralelogramo com a diagonal mais longa (b) como base e metade da diagonal mais curta (a) como altura. Assim, a área torna-se b * a = ab. Uma abordagem mais complicada envolve um pouco de álgebra. Corte a pipa na diagonal mais curta para formar dois triângulos com a diagonal mais curta (a) como base. Assim, a área do primeiro triângulo é a * squiggly, onde squiggly é a altura. A área do segundo triângulo é a * (b – squiggly), onde (b – squiggly) é a parte restante da diagonal mais longa. A área total torna-se assim ( a * squiggly) + ( a * (b – squiggly)). Fatorando a, temos a (squiggly + b – squiggly) = ab.

Bem, o que você sabe. Basicamente, você só precisa saber a fórmula para a área de um paralelogramo e derivar a fórmula para os outros.