Distribuição exponencial
por Marco Taboga, PhD
A distribuição exponencial é uma distribuição de probabilidade contínua usada para modelar o tempo que precisamos esperar antes que um determinado evento ocorra. É a contraparte contínua da distribuição geométrica, que é discreta.
Às vezes, também é chamada de distribuição exponencial negativa.
Introdução
Quanto tempo vai decorrer antes que um terremoto ocorra em uma determinada região? Quanto tempo precisamos esperar até que um cliente entre em nossa loja? Quanto tempo leva para que um call center receba a próxima ligação? Por quanto tempo uma peça de máquina trabalhará sem quebrar?
Perguntas como essas são frequentemente respondidas em termos probabilísticos, usando a distribuição exponencial.
Todas essas perguntas dizem respeito ao tempo de que precisamos esperar antes que um determinado evento ocorra. Se esse tempo de espera for desconhecido, geralmente é apropriado pensar nele como uma variável aleatória com uma distribuição exponencial.
Falando de maneira geral, o tempo 
de que precisamos esperar antes que um evento ocorra tem uma distribuição exponencial se a probabilidade de o evento ocorrer durante um determinado intervalo de tempo for proporcional à duração desse intervalo de tempo.
Mais precisamente, tem uma distribuição exponencial se a probabilidade condicional for aproximadamente proporcional ao comprimento do intervalo de tempo compreendido entre os tempos e , para qualquer instante .
Em muitas situações práticas, essa propriedade é muito realista. Esta é a razão pela qual a distribuição exponencial é tão amplamente usada para modelar tempos de espera.
A distribuição exponencial está estritamente relacionada à distribuição de Poisson. Se 1) um evento pode ocorrer mais de uma vez e 2) o tempo decorrido entre duas ocorrências sucessivas é distribuído exponencialmente e independente de ocorrências anteriores, então o número de ocorrências do evento em uma determinada unidade de tempo tem uma distribuição de Poisson. Convidamos o leitor a ver a palestra sobre a distribuição de Poisson para uma explicação mais detalhada e uma representação gráfica intuitiva desse fato.
Definição
A distribuição exponencial é caracterizada da seguinte maneira.
Definição Seja uma variável aleatória contínua. Seja seu suporte o conjunto de números reais positivos: Let . Dizemos que tem uma distribuição exponencial com o parâmetro se e somente se sua função de densidade de probabilidade for O parâmetro é chamado de parâmetro de taxa.
Uma variável aleatória com uma distribuição exponencial também é chamada de variável aleatória exponencial.
O que se segue é uma prova de que é uma função de densidade de probabilidade legítima.
A não negatividade é óbvia. Precisamos provar que a integral de sobre é igual a . Isso é provado da seguinte forma:
Para entender melhor a distribuição exponencial, você pode dar uma olhada em seus gráficos de densidade.
O parâmetro da taxa e sua interpretação
Mencionamos que a probabilidade de o evento ocorrer entre duas datas e é proporcional a (condicional à informação de que não ocorreu antes de ). O parâmetro de taxa é a constante de proporcionalidade: onde é um infinitesimal de ordem superior a (ou seja, uma função de que vai para zero mais rapidamente do que faz).
A condição de proporcionalidade acima também é suficiente para caracterizar completamente a distribuição exponencial.
Proposição A condição de proporcionalidade é satisfeito apenas se tiver uma distribuição exponencial.
A probabilidade condicional pode ser escrita como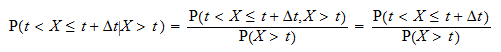 
Denote por a função de distribuição de , isto é, e por sua função de sobrevivência: Então, Dividindo os dois lados por , obtemos onde é uma quantidade que tende a quando tende a . Tomando limites em ambos os lados, obtemos ou, pela definição de derivada: Esta equação diferencial é facilmente resolvida usando a cadeia regra: Pegando a integral de para de ambos os lados, obtemos e ou Mas (porque não pode aceitar valores negativos) implica Exponenciando ambos os lados, obtemos Portanto, ou Mas a função de densidade é a primeira derivada da função de distribuição: e o termo mais à direita é a densidade de uma variável aleatória exponencial. Portanto, a condição de proporcionalidade é satisfeita apenas se for uma variável aleatória exponencial
Valor esperado
O valor esperado de uma variável exponencial aleatória é
Pode ser derivado da seguinte forma: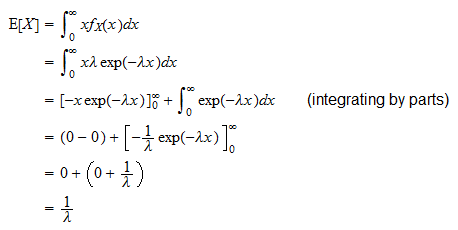 
Variância
A variância de um a variável aleatória exponencial é
Isso pode ser derivada graças à fórmula de variação usual (): 
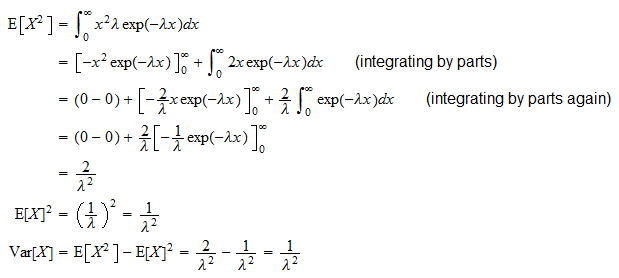
Função de geração de momento
A função de geração de momento de uma variável exponencial aleatória é definida para qualquer :
A definição de função geradora de momento fornece De Claro, os integrais acima convergem apenas se , ou seja, apenas se . Portanto, a função geradora de momento de uma variável aleatória exponencial existe para todos os .
Função característica
A função característica de uma variável aleatória exponencial é
Usando a definição de função característica e o fato de que podemos escrever Agora calculamos separadamente as duas integrais . A primeira integral é 
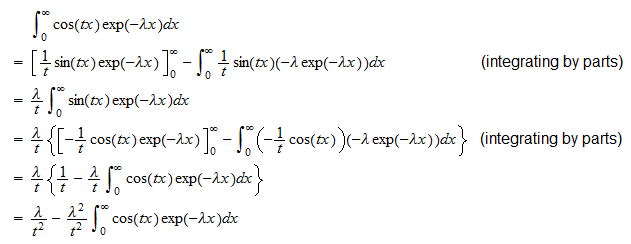Portanto, que pode ser reorganizada para render ou O segundo integral é 
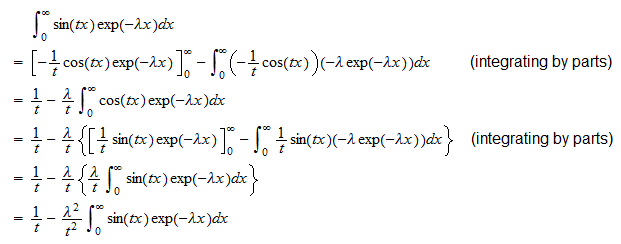Portanto, que pode ser reorganizado para render ou Ao juntar as peças, obtemos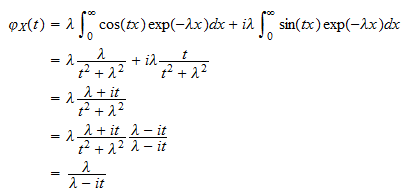 
Função de distribuição
A função de distribuição de uma variável aleatória exponencial é
Se , então porque não pode assumir valores negativos. Se , então
Mais detalhes
Nas subseções a seguir, você pode encontrar mais detalhes sobre a distribuição exponencial.
Propriedade sem memória
Uma das propriedades mais importantes da distribuição exponencial é a propriedade sem memória: para qualquer .
Isso é provado da seguinte maneira: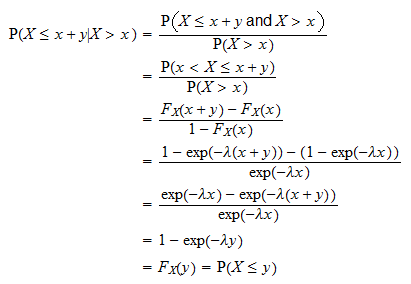 
é o tempo que precisamos esperar antes de um determinado evento ocorre. A propriedade acima diz que a probabilidade de o evento acontecer durante um intervalo de tempo de duração é independente de quanto tempo já passou () sem que o evento aconteça.
A soma das variáveis aleatórias exponenciais é uma variável aleatória Gamma
Suponha , , …, são variáveis aleatórias mutuamente independentes com distribuição exponencial com parâmetro .
Defina
Então, a soma é uma variável aleatória Gamma com parâmetros e .
Isso é provado usando o momento funções geradoras (lembre-se de que a função geradora de momento de uma soma de variáveis aleatórias independentes entre si é apenas o produto de suas funções geradoras de momento): A última é a função geradora de momento de um Gama distribuição com parâmetros e . Portanto, tem uma distribuição Gama, porque duas variáveis aleatórias têm a mesma distribuição quando têm a mesma função de geração de momento.
A variável aleatória também é algumas vezes considerada como tendo uma distribuição Erlang. A distribuição Erlang é apenas um caso especial da distribuição Gamma: uma variável aleatória Gamma também é uma variável aleatória Erlang quando pode ser escrita como uma soma de variáveis aleatórias exponenciais.
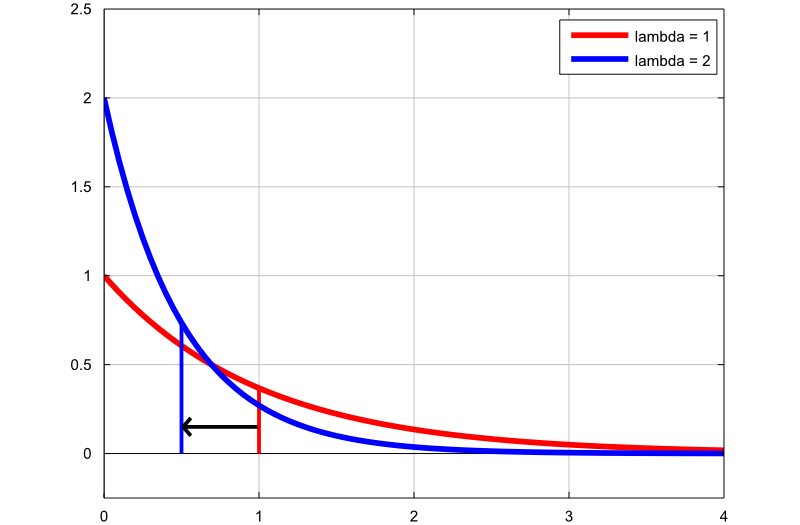
Gráfico de densidade
O próximo gráfico mostra como a densidade da distribuição exponencial muda ao alterar o parâmetro de taxa:
-
o primeiro gráfico (linha vermelha) é a função de densidade de probabilidade de uma variável exponencial aleatória com parâmetro de taxa
; -
o segundo gráfico (linha azul) é a função de densidade de probabilidade de uma variável aleatória exponencial com parâmetro de taxa
.
As linhas verticais finas indicam as médias das duas distribuições. Observe que, ao aumentar o parâmetro de taxa, diminuímos a média da distribuição de para .
Exercícios resolvidos
Abaixo, você pode encontrar alguns exercícios com soluções explicadas.
Exercício 1
Seja uma variável aleatória exponencial com parâmetro . Calcule a seguinte probabilidade:
Em primeiro lugar, podemos escrever a probabilidade como usando o fato de que a probabilidade de uma variável aleatória contínua assumir qualquer valor específico é igual a zero (consulte Variáveis aleatórias contínuas e eventos de probabilidade zero). Agora, a probabilidade pode ser escrita em termos da função de distribuição de como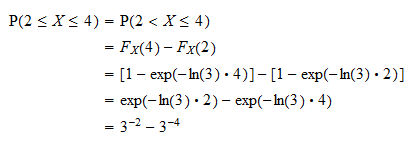 
Exercício 2
Suponha que a variável aleatória tenha uma distribuição exponencial com o parâmetro . Calcule a seguinte probabilidade:
Esta probabilidade pode ser facilmente calculada usando a função de distribuição de :
Exercício 3
Qual é a probabilidade de uma variável aleatória é menor que seu valor esperado, se tiver uma distribuição exponencial com parâmetro ?
O valor esperado de uma variável aleatória exponencial com o parâmetro é A probabilidade acima pode ser calculada usando a função de distribuição de :
Como citar
Por favor, cite como: