Distribuição de Poisson
Dado um processo de Poisson, a probabilidade de obter exatamente 
sucessos em 
tentativas é dada pelo limite de uma distribuição binomial
 |
(1)
|
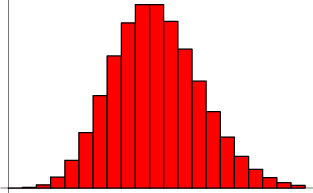
Visualização da distribuição como uma função do número esperado de sucessos
 |
(2)
|
em vez do tamanho da amostra 
para 
fixa, a equação (2) torna-se
 |
(3)
|
Deixando o tamanho da amostra 
aumentar, a distribuição se aproxima de
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
que é conhecida como distribuição de Poisson (Papoulis 1984, pp. 101 e 554; Pfeiffer e Schum 1973, p. 200). Observe que o tamanho da amostra 
saiu completamente da função de probabilidade, que tem a mesma forma funcional para todos os valores de 
.
 |
(9 )
|
A razão de probabilidades é dada por
 |
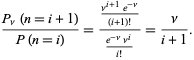(10)
|
A distribuição de Poisson atinge o máximo quando
 |
(11)
|
onde é a constante de Euler-Mascheroni e 
é um número harmônico, levando à equação transcendental
 |
(12)
|
que não pode ser resolvido exatamente para 
.
A função de geração de momento da distribuição de Poisson é fornecida por
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
então
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, p. 554).
Os momentos brutos também podem ser calculados diretamente por soma, o que produz uma conexão inesperada com o polinômio de Bell 
e números de Stirling de segundo tipo,
 |
(21)
|
conhecida como fórmula de Dobiński.Portanto,
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
Os momentos centrais podem então ser calculados como
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
então o excesso de média, variância, assimetria e curtose são
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
A função característica para a distribuição Poissond é
(Papoulis 1984, pp. 154 e 554), e a função geradora de cumulante é
 |
(34)
|
então
 |
(35)
|
O desvio médio da distribuição de Poisson é dado por
 |
(36)
|
A distribuição de Poisson também pode ser expressa em termos de
 |
(37)
|
 |
(38)
|
A função geradora de momento de uma distribuição de Poisson em duas variáveis é fornecida por
 |
(39)
|
Se as variáveis independentes 
, 
, …, 
têm distribuições de Poisson com parâmetros 
, 
, …, 
e, em seguida,
 |
(40)
|
tem uma distribuição Poisson com o parâmetro
 |
(41)
|
Isso pode ser visto porque a função geradora de cumulantes é
 |
(42)
|
 |
(43)
|
Uma generalização da distribuição de Poisson foi usada por Saslaw (1989) para modelar o agrupamento observado de galáxias no universo. A forma dessa distribuição é fornecida por
|
(44)
|
onde 
é o número de galáxias em um volume 
, 
, 
é a densidade média de galáxias, e 
, com 
é a proporção da energia gravitacional para a cinética energia de movimentos peculiares, Letting 
dá
 |
(45)
|
que é de fato uma distribuição de Poisson com 
. Da mesma forma, deixar 
dá 
.