Como calcular o volume

Calculando o volume

O volume é medido em cubos (ou unidades cúbicas).

Quantos cubos existem neste prisma retangular (cubóide)?

Podemos contar os cubos, embora seja mais rápido pegar o comprimento, largura e altura e usar a multiplicação. O prisma retangular acima tem um volume de 48 unidades cúbicas.

O volume de um prisma retangular é = comprimento x largura x altura

Exemplos de cálculo da área de um retângulo

Precisamos fazer duas multiplicações para calcular o volume. Calculamos a área de uma face (ou lado) e multiplicamos por sua altura. Os exemplos abaixo mostram como existem três maneiras de fazer isso.

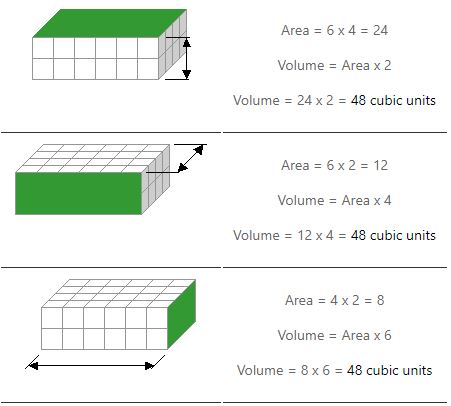
Observe como obtemos a mesma resposta, independentemente do lado que usamos para encontrar uma área.

Quando seu filho começa a trabalhar com a área e o perímetro, ele normalmente trabalhará com 2 dimensões – quadrados, retângulos, triângulos, etc. que são mostrados no papel como planos – não há profundidade ou 3ª dimensão. Trabalhar com volume envolve 3 dimensões. Certifique-se de que seu filho está ciente disso e não pensa nos cubos e outras formas 3D mostradas no papel como sendo apenas mais uma “forma na página”. Mostre-lhes caixas reais e mostre como elas podem ser desenhadas (ou representadas) em uma folha de papel bidimensional. Em outras palavras, certifique-se de que a conexão entre o que está no papel e o que ele representa no mundo real seja feita.

Certifique-se de que seu filho não se confunda com o uso do volume quando se fala sobre volume .

Unidades para medir o volume

Existem diferenças muito grandes entre as unidades de medida para o volume. Por exemplo, existem 100 centímetros em 1 metro, mas existem 1.000.000 (sim, 1 milhão ) centímetros cúbicos em um metro cúbico.

Por que a grande diferença? Porque em volume não temos apenas comprimento; temos comprimento, largura e altura. O exemplo do cubo de açúcar abaixo mostra isso.

Quanto açúcar? 1 m3 ou 1.000.000 cm3

Pense em encher uma caixa muito grande (teria 1 metro de largura, 1 metro de comprimento e um metro de altura) com cubos de açúcar (com cada lado 1 centímetro).

	Etapa 1: uma linha ao longo da parte inferior da caixa – isso seria 100 cubos de açúcar
	Etapa 2: cubra o resto da base da caixa – isso daria um total de 100 linhas cada com 100 cubos de açúcar. 100 x 100 = 10.000 cubos de açúcar no fundo da caixa grande.
	Etapa 3: Repita 99 vezes até que haja camadas de 10.000 cubos empilhados 100 de profundidade. 10.000 x 100 = 1.000.000 de cubos de açúcar

Existem 1.000.000 cm3 em 1 m3 – tome cuidado para não ter muito açúcar!

Existem outras unidades para medir o volume; polegadas cúbicas, pés cúbicos, jardas cúbicas são todas as unidades usadas para medir o volume. Mililitros, litros, galões também são usados especialmente para medir líquidos.

Não se esqueça do pequenino 3

Escrevemos tamanhos cúbicos usando um pequeno 3 ao lado da unidade.
Escrevemos mm3, cm3, m3, km3, cm3
Podemos dizer “85 centímetros cúbicos” ou “85 centímetros cúbicos”

Exemplos de cálculo de volume de prismas retangulares

	Volume = Comprimento x Largura x Altura Volume = 12 cm x 8 cm x 6 cm = 576 cm3
		Volume = Comprimento x Largura x Altura Volume = 20 mx 2 mx 2 m = 80 m3
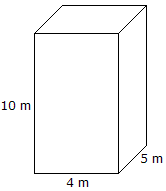	Volume = Comprimento x Largura x Altura Volume = 10 mx 4 mx 5 m = 200 m3

Volume de um cilindro

Calculando o volume de um cilindro der envolve multiplicar a área da base pela altura do cilindro. A base de um cilindro é circular e a fórmula para a área de um círculo é: área de um círculo = πr2. Há mais aqui na área de um círculo.

Volume = Área da base x Altura Volume = πr2 xh Volume = πr2 h

Observação: nos exemplos abaixo usaremos 3,14 como um valor aproximado para π (Pi).

Exemplo de cálculo do volume de um cilindro

As dimensões estão em cm.

Volume = πr2 h Volume = 3.14 x 3 x 3 x 8 Volume = 226,08 cm3

Volume de um cone

O volume de um cone é igual a um terço do volume de um cilindro com altura e área de base correspondentes. Isso dá a fórmula para o volume de um cone, conforme mostrado abaixo.

Volume = 1/3 πr2h

Exemplo de cálculo do volume de um cone

As dimensões estão em cm.

Volume = 1/3 πr2 h Volume = 1/3 x 3,14 x 2 x 2 x 7 Volume = 29,31 cm3

Volume de uma esfera

A fórmula para o volume de uma esfera é mostrada abaixo.

Volume = 4/3 πr3

Exemplo de cálculo do volume de uma esfera

As dimensões estão em cm.

Volume = 4/3 πr3 Volume = 4/3 x 3,14 x 4 x 4 x 4 Volume = 267,95 cm3

Planilhas de volume para impressão

Use a planilha abaixo para praticar o cálculo de volumes.

• Encontrando o volume em unidades cúbicas – prismas retangulares e composições
• Volumes de prismas retangulares
• Volumes de prismas retangulares
• Volumes de objetos do “mundo real”, por exemplo de caixas de cereais
• Cálculo de volumes, por exemplo de prismas triangulares e cilindros

Você obterá outras planilhas de geometria sobre perímetro, área e muito mais aqui.