Como calcular a área

Calculando a área

A área é medida em quadrados (ou unidades quadradas).

Quantos quadrados existem neste retângulo?

Podemos contar os quadrados ou podemos pegue o comprimento e a largura e use a multiplicação. O retângulo acima tem uma área de 15 unidades quadradas.

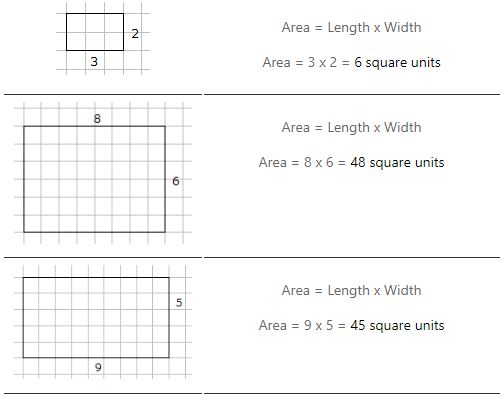
A área de um retângulo é = comprimento x largura

Exemplos de cálculo da área de um retângulo

Unidades para medir área

Nós medimos a área usando quadrados. Usamos tamanhos diferentes de quadrados, dependendo do tamanho da área.

Exemplo	Comprimento do lado nos quadrados	Unidade
Tamanho do unha no polegar	Milímetro	mm2
Tamanho do pedaço de papel	Centímetro	cm2
Tamanho de uma sala	Medidor	m2
Tamanho de uma cidade	Quilômetro	km2

Não se esqueça do pequenino 2

Escrevemos os tamanhos quadrados usando um pequeno 2 ao lado da unidade.
Escrevemos mm2, cm2, m2, km2, cm2
Podemos dizer “63 milímetros quadrados” ou “63 milímetros quadrados”

Poderíamos usar pequenos quadrados para medir áreas grandes. O único problema com isso é que acabaríamos tendo que usar muito grandes números. Por exemplo, um campo pode ser medido em 5.000.000.000 de milímetros quadrados, quando 5.000 metros quadrados seria um tamanho muito mais fácil de dizer, escrever e visualizar.

Você provavelmente ouvirá mais unidades para medir a área; polegadas quadradas, pés quadrados, jardas quadradas, milhas quadradas, acres, hectares são todas as unidades usadas para medir a área.

Mais exemplos de cálculo de área

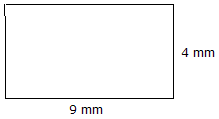	Área = Comprimento x Largura Área = 9 mm x 4 mm = 36 mm2
	Área = Comprimento x Largura Área = 7 cm x 6 cm = 42 cm2
	Área = Comprimento x Largura Área = 8 mx 2 m = 16 m2
	Área = Comprimento x Largura Área = 7 km x 5 km = 35 km2

Área de um quadrado

O comprimento e a largura de um quadrado são iguais, então precisamos apenas multiplicar o comprimento pelo comprimento.

Área = Comprimento x Comprimento Área = 6 cm x 6 cm = 36 cm2

Área de um círculo

A área de um círculo = πr2
onde r é o raio do círculo e π é a razão entre a circunferência de um círculo e seu diâmetro.

π (pronuncia-se “torta” e geralmente é escrito como “Pi”) é um decimal infinito com um comum aproximação de 3,14159. Você pode descobrir mais sobre Pi aqui

Exemplo de cálculo da área de um círculo

Área = πr2 Área = 3,14159 x (4 cm) 2 Área = 3,14159 x 16 cm2 Área = 50,27 cm2 Resposta arredondada para 2 casas decimais

Explicação da área de uma fórmula de círculo

Pegue um círculo e divida-o em setores de tamanhos iguais e reorganize-os conforme mostrado abaixo. Observe como, à medida que os setores ficam menores, a forma fica mais parecida com um retângulo. Nota: Não há limite para o quão pequenos esses setores podem ser e até que ponto eles podem se parecer com um retângulo quando organizados.

Supondo que saibamos que a circunferência de um círculo é igual a 2πr, podemos adicionar dimensões o “retângulo” conforme mostrado abaixo. Usando a fórmula da área de uma área de retângulo, área = largura x altura, podemos ver como nosso círculo, reconfigurado como um retângulo, pode ter uma área que se aproxima de πr xr ou πr2

Círculo Setores reorganizados

Setores do círculo reorganizados – começando ter a aparência de um retângulo

Área de Formas compostas

Existem muitos casos em que o cálculo de uma área total requer que mais de uma área seja calculada seguida por uma adição, subtração ou alguma outra combinação de operações para encontrar a área necessária.

Nota: Nos exemplos abaixo as unidades de medida não são mostradas e as respostas e o valor de π (Pi) foram arredondados para o centésimo mais próximo.

Exemplo: Formas compostas simples

O exemplo de cálculo de área abaixo é relativamente simples. A forma pode ser vista como um triângulo combinado com um retângulo.

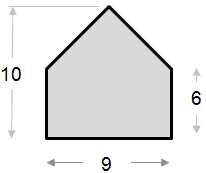Área da parte do triângulo: ½ x base x altura ½ x 9 x 4 = 18 Área da parte do retângulo: largura x altura 9 x 6 = 54 Área total = 18 + 54 = 72

O exemplo acima ilustra um requisito comum ao trabalhar com compostos formas – encontrar dimensões que não são mostradas. Ao dar aulas particulares a seus filhos, ajude, quando necessário, a encontrar essas dimensões “ausentes”. Há outro exemplo abaixo.

Encontrar as dimensões

Quais são as dimensões da pequena peça retangular? Largura? 12 – 7 – 2 = 3 Altura? 8 – 6 = 2

Exemplo: subtraindo uma área de outra

No exemplo abaixo, a forma pode ser vista como um retângulo com um corte de triângulo.

Área da parte do retângulo: largura x altura 5 x 6 = 30 Área da parte do triângulo: ½ x base x altura ½ x 3 x 3 = 4,50 Área total = 30 – 4,50 = 25,50

Exemplo: áreas parciais

O exemplo abaixo é semelhante ao anterior, embora, como temos um semicírculo, precisamos calcular uma fração (metade) da área do círculo. Observe neste exemplo o diâmetro, e não o raio, é mostrado.

Área da parte do triângulo: ½ x base x altura ½ x 6 x 6 = 18 Área da parte do semicírculo: ½ x (πr2) ½ x (3,14 x 1,52) = 3,53 Área total = 18 – 3,53 = 14,47

Exemplo: Decisões! Combinar? Subtrair

É comum haver mais de uma forma de calcular a área final. Nos exemplos abaixo, a forma pode ser vista como dois retângulos combinados ou como um grande retângulo com um retângulo menor “recortado” no canto superior direito.

Calculando planilhas de área

Imprimir extraia as planilhas listadas abaixo e use-as para praticar ao dar aulas a seus filhos.

• Áreas de cálculo – retângulos e quadrados
• Áreas de cálculo – retângulos
• Áreas – retângulos
• Cálculo de áreas compostas, por exemplo com formas retangulares
• Calculando áreas compostas, por exemplo com retângulos, triângulos e círculos
• Calculando áreas, por exemplo de triângulos
• Área de um círculo
• Cálculo de áreas de superfície, por exemplo de prismas retangulares

Você encontrará mais planilhas de geometria para impressão aqui.