Álgebra universitária (Português)
Observando o gráfico de uma função racional, podemos investigar seu comportamento local e ver facilmente se há assíntotas. Podemos até ser capazes de aproximar sua localização. Mesmo sem o gráfico, no entanto, ainda podemos determinar se uma determinada função racional tem alguma assíntota e calcular sua localização.
Assíntotas verticais
As assíntotas verticais de uma função racional podem ser encontrado examinando os fatores do denominador que não são comuns aos fatores do numerador. Assíntotas verticais ocorrem nos zeros desses fatores.
Como: Dada uma função racional, identifique quaisquer assíntotas verticais de seu gráfico.
- Fatore o numerador e denominador.
- Observe todas as restrições no domínio da função.
- Reduza a expressão cancelando fatores comuns no numerador e no denominador.
- Observe quaisquer valores que fazem com que o denominador seja zero nesta versão simplificada. É aqui que ocorrem as assíntotas verticais.
- Observe quaisquer restrições no domínio onde as assíntotas não ocorrem. Estas são descontinuidades removíveis.
Descontinuidades removíveis
Ocasionalmente, um gráfico conterá um buraco: um único ponto onde o gráfico não é definido, indicado por um círculo aberto. Chamamos esse buraco de descontinuidade removível.
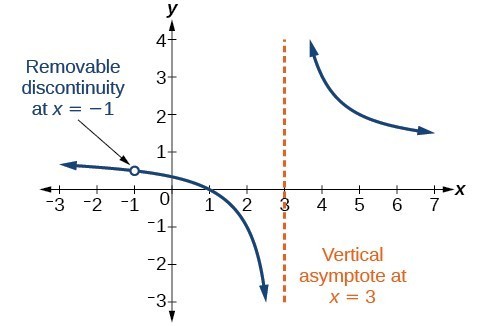
Figura 10
Uma observação geral: descontinuidades removíveis de funções racionais
Uma descontinuidade removível ocorre no gráfico de uma função racional em x = a se a for zero para um fator no denominador que é comum a um fator no numerador. Fatoramos o numerador e o denominador e verificamos os fatores comuns. Se encontrarmos algum, definimos o fator comum igual a 0 e resolvemos. Este é o local da descontinuidade removível. Isso é verdadeiro se a multiplicidade desse fator for maior ou igual à do denominador. Se a multiplicidade deste fator for maior no denominador, então ainda há uma assíntota nesse valor.
Assíntotas horizontais
Enquanto as assíntotas verticais descrevem o comportamento de um gráfico conforme a saída fica muito grande ou muito pequena, as assíntotas horizontais ajudam a descrever o comportamento de um gráfico conforme a entrada fica muito grande ou muito pequena. Lembre-se de que o comportamento final de um polinômio refletirá o do termo líder. Da mesma forma, o comportamento final de uma função racional espelhará o da proporção dos termos principais das funções do numerador e do denominador.
Existem três resultados distintos ao verificar as assíntotas horizontais:
Caso 1: Se o grau do denominador > grau do numerador, há uma assíntota horizontal em y = 0.

Caso 2: Se o grau do denominador < grau do numerador por um, obtemos uma assíntota inclinada.

Observe que, embora o gráfico de uma função racional nunca cruze uma assíntota vertical, o gráfico pode ou não cruzar uma horizontal ou assíntota inclinada. Além disso, embora o gráfico de uma função racional possa ter muitas assíntotas verticais, o gráfico terá no máximo uma assíntota horizontal (ou inclinada).
Deve-se notar que, se o grau do numerador for maior do que o grau do denominador por mais de um, o comportamento final do gráfico irá imitar o comportamento da fração reduzida do comportamento final. Por exemplo, se tivéssemos a função
com comportamento final
o comportamento final do gráfico seria semelhante ao de um polinômio par com um coeficiente líder positivo.
Uma observação geral: Assíntotas horizontais de Funções racionais
A assíntota horizontal de uma função racional pode ser determinada observando os graus do numerador e denominador.
- O grau do numerador é menor que o grau do denominador: assíntota horizontal em y = 0.
- O grau do numerador é maior do que o grau do denominador por um: sem assíntota horizontal; assíntota inclinada.
- O grau do numerador é igual ao grau do denominador: assíntota horizontal na proporção dos coeficientes principais.
Uma Nota Geral: Interceptações de Funções Racionais
Uma função racional terá uma interceptação em y quando a entrada for zero, se o função é definida em zero. Uma função racional não terá interceptação y se a função não for definida em zero.
Da mesma forma, uma função racional terá interceptações x nas entradas que fazem com que a saída seja zero. Como uma fração só é igual a zero quando o numerador é zero, as interceptações x só podem ocorrer quando o numerador da função racional é igual a zero.
Experimente 7
Dada a função quadrada recíproca que é deslocada para a direita 3 unidades e para baixo 4 unidades, escreva isso como uma função racional. Em seguida, encontre as interceptações x e y e as assíntotas horizontais e verticais.
Solução