Poisson-Verteilung
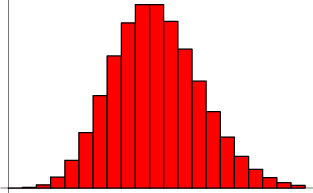
Bei einem Poisson-Prozess ist die Wahrscheinlichkeit, in 
-Versuchen genau 
Erfolge zu erzielen, durch die Grenze einer Binomialverteilung
 |
(1)
|
Anzeigen der Verteilung als Funktion der erwarteten Anzahl von Erfolgen
 |
(2)
|
anstelle der Stichprobengröße 
für festes 
wird Gleichung (2) dann zu
 |
(3)
|
Wenn die Stichprobengröße 
groß wird, nähert sich die Verteilung
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
, bekannt als Poisson-Verteilung (Papoulis 1984, S. 101 und 554; Pfeiffer und Schum 1973, p. 200). Beachten Sie, dass die Stichprobengröße 
vollständig aus der Wahrscheinlichkeitsfunktion herausgefallen ist, die für alle Werte von 
dieselbe funktionale Form hat.
Die Poisson-Verteilung wird in der WolframLanguage als PoissonDistribution implementiert.
Wie erwartet wird die Poisson-Verteilung so normalisiert, dass die Summe der Wahrscheinlichkeiten gleich 1 ist, da
 |
(9 )
|
Das Wahrscheinlichkeitsverhältnis wird durch
 |
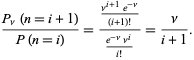(10)
|
Die Poisson-Verteilung erreicht ein Maximum, wenn
 |
(11)
|
wobei ist die Euler-Mascheroni-Konstante und 
ist eine harmonische Zahl, die zur transzendentalen Gleichung
, die nicht genau für 
gelöst werden kann.
Die momentgenerierende Funktion der Poisson-Verteilung ist gegeben durch
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
also
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, p. 554).
Die Rohmomente können auch direkt durch Summation berechnet werden, was eine unerwartete Verbindung mit dem Bell-Polynom 
und Stirling-Zahlen der zweiten Art ergibt.
 |
(21)
|
bekannt als Dobińskis Formel.Daher
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
Die zentralen Momente können dann als
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
Mittelwert, Varianz, Schiefe und Kurtosisüberschuss sind also
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
Die charakteristische Funktion für die Poissondistribution ist
(Papoulis 1984, S. 154 und 554), und die Funktion zur Erzeugung von Kumulanten ist
 |
(34)
|
also
 |
(35)
|
Die mittlere Abweichung der Poisson-Verteilung wird durch
 |
(36)
|
Die Poisson-Verteilung kann auch als
 |
(37)
|
 |
(38)
|
Die momenterzeugende Funktion der Poisson-Verteilung in zwei Variablen wird durch
angegeben  |
(39)
|
Wenn die unabhängigen Variablen 
, 
, …, 
haben Poisson-Verteilungen mit den Parametern 
, 
, …, 
, dann
 |
(40)
|
hat eine Poisson-Verteilung mit dem Parameter
 |
(41)
|
Dies ist zu sehen, da die Funktion zur Erzeugung von Kumulanten
|
(42)
|
 |
(43)
|
Eine Verallgemeinerung der Poisson-Verteilung wurde von Saslaw (1989) zur Modellierung verwendet die beobachtete Häufung von Galaxien im Universum. Die Form dieser Verteilung wird durch
 |
(44)
|
wobei 
ist die Anzahl der Galaxien in einem Volumen 
, 
, 
ist die durchschnittliche Dichte von Galaxien und 
mit 
ist das Verhältnis von Gravitationsenergie zu Kinetik Energie von besonderen Bewegungen. Wenn Sie 
lassen, erhalten Sie
 |
(45)
|
Dies ist in der Tat eine Poisson-Distribution mit 
. In ähnlicher Weise ergibt das Teilen von 
.