Rozkład wykładniczy
autorstwa dr Marco Tabogi
Rozkład wykładniczy to ciągły rozkład prawdopodobieństwa używany do modeluj czas, jaki musimy czekać, zanim wystąpi dane zdarzenie. Jest to ciągły odpowiednik rozkładu geometrycznego, który jest zamiast tego dyskretny.
Czasami nazywany jest również ujemnym rozkładem wykładniczym.
Wprowadzenie
Ile czasu minie, zanim nastąpi trzęsienie ziemi w danym regionie? Jak długo musimy czekać, aż klient wejdzie do naszego sklepu? Jak długo potrwa, zanim call center otrzyma następny telefon? Jak długo maszyna będzie działać bez awarii?
Na pytania takie jak te często odpowiada się w kategoriach probabilistycznych, używając rozkładu wykładniczego.
Wszystkie te pytania dotyczą czasu, którego potrzebujemy. czekać, zanim nastąpi dane wydarzenie. Jeśli ten czas oczekiwania jest nieznany, często dobrze jest myśleć o nim jako o zmiennej losowej o rozkładzie wykładniczym.
Z grubsza rzecz biorąc, czas 
, którego potrzebujemy oczekiwanie na wystąpienie zdarzenia ma rozkład wykładniczy, jeśli prawdopodobieństwo wystąpienia zdarzenia w określonym przedziale czasu jest proporcjonalne do długości tego przedziału czasu.
Dokładniej, ma rozkład wykładniczy, jeśli prawdopodobieństwo warunkowe jest w przybliżeniu proporcjonalne do długości przedziału czasowego zawartego między czasami i , w dowolnym momencie .
W wielu praktycznych sytuacjach ta właściwość jest bardzo realistyczna. To jest powód, dla którego rozkład wykładniczy jest tak szeroko stosowany do modelowania czasów oczekiwania.
Rozkład wykładniczy jest ściśle powiązany z rozkładem Poissona. Jeżeli 1) zdarzenie może wystąpić więcej niż raz i 2) czas, który upłynął między dwoma kolejnymi wystąpieniami, jest rozkładem wykładniczym i niezależny od poprzednich, to liczba wystąpień zdarzenia w danej jednostce czasu ma rozkład Poissona. Zapraszamy czytelnika do obejrzenia wykładu na temat rozkładu Poissona w celu dokładniejszego wyjaśnienia i intuicyjnego graficznego przedstawienia tego faktu.
Definicja
Rozkład wykładniczy jest scharakteryzowany w następujący sposób.
Definicja Niech będzie ciągłą zmienną losową. Niech jego wsparcie będzie zbiorem dodatnich liczb rzeczywistych: Niech . Mówimy, że ma rozkład wykładniczy z parametrem wtedy i tylko wtedy, gdy jego funkcja gęstości prawdopodobieństwa wynosi Parametr nazywa się parametrem szybkości.
Zmienna losowa o rozkładzie wykładniczym jest również nazywana wykładniczą zmienną losową.
Poniżej znajduje się dowód na to, że jest uzasadnioną funkcją gęstości prawdopodobieństwa.
Brak negatywności jest oczywisty. Musimy udowodnić, że całka z po jest równa . Jest to udowodnione w następujący sposób:
Aby lepiej zrozumieć rozkład wykładniczy, możesz przyjrzeć się jego wykresom gęstości.
Parametr rate i jego interpretacja
Wspomnieliśmy, że prawdopodobieństwo wystąpienia zdarzenia między dwiema datami i jest proporcjonalne do (zależnie od informacji, że nie wystąpiło przed ). Parametr szybkości jest stałą proporcjonalności: gdzie jest nieskończenie małą liczbą wyższego rzędu niż (tj. funkcja , która znika do zera szybciej niż robi).
Powyższy warunek proporcjonalności jest również wystarczający do pełnego scharakteryzowania rozkładu wykładniczego.
Twierdzenie Warunek proporcjonalności jest spełnione tylko wtedy, gdy ma rozkład wykładniczy.
Prawdopodobieństwo warunkowe można zapisać jako 
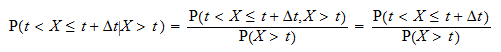Oznacz przez funkcję dystrybucji , czyli i przez swoją funkcję przetrwania: Następnie Dzieląc obie strony przez , otrzymujemy gdzie to wielkość, która ma tendencję do , gdy ma tendencję do . Biorąc granice po obu stronach, otrzymujemy lub, zgodnie z definicją pochodnej: To równanie różniczkowe można łatwo rozwiązać za pomocą łańcucha reguła: Biorąc całkę z do z obu stron, otrzymujemy i lub Ale (ponieważ nie może przyjmować wartości ujemnych) oznacza, że potęgując obie strony, otrzymujemy Dlatego lub Ale funkcja gęstości jest pierwszą pochodną funkcji rozkładu: , a skrajnie prawy wyraz to gęstość wykładniczej zmiennej losowej. Dlatego warunek proporcjonalności jest spełniony tylko wtedy, gdy jest wykładniczą zmienną losową
Wartość oczekiwana
Oczekiwana wartość wykładniczej zmiennej losowej to
Można ją wyprowadzić w następujący sposób: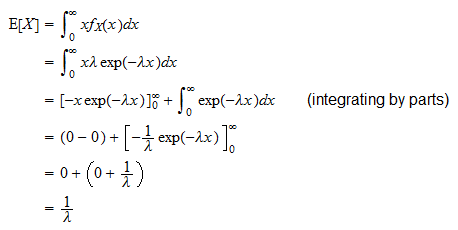 
Wariancja
Wariancja wykładnicza zmienna losowa to
To można wyprowadzić dzięki zwykłej formule wariancji (): 
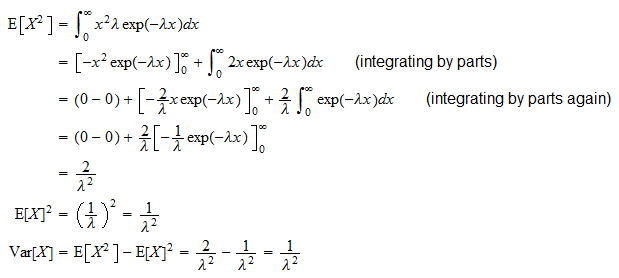
Funkcja generująca moment
Funkcja generująca moment wykładniczej zmiennej losowej jest zdefiniowana dla dowolnego :
Definicja funkcji generującej moment daje Of Oczywiście powyższe całki zbiegają się tylko wtedy, gdy , czyli tylko wtedy, gdy . Dlatego funkcja generująca moment wykładniczej zmiennej losowej istnieje dla wszystkich .
Funkcja charakterystyczna
Charakterystyczną funkcją wykładniczej zmiennej losowej jest
Korzystając z definicji funkcji charakterystycznej i faktu, że możemy napisać Teraz obliczamy osobno dwie całki . Pierwsza całka to 
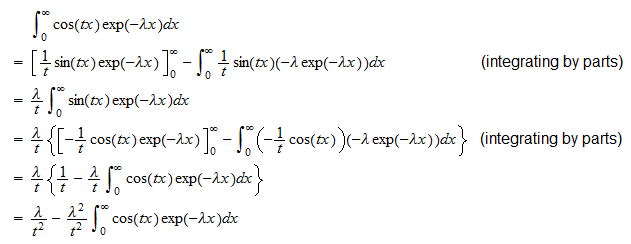W związku z tym można zmienić kolejność, aby uzyskać lub Druga całka to 
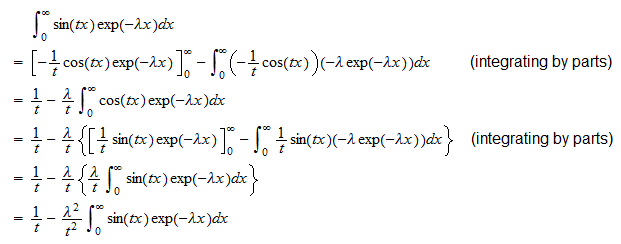W związku z tym można zmienić kolejność, aby uzyskać lub Po złożeniu elementów otrzymujemy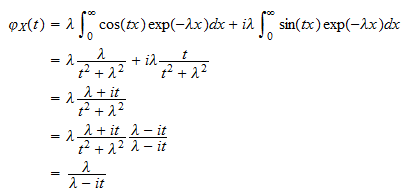 
Funkcja rozkładu
Funkcja rozkładu wykładniczej zmiennej losowej to
Jeśli , to , ponieważ nie może przyjmować wartości ujemnych. Jeśli , to
Więcej szczegółów
W następnych podrozdziałach można znaleźć więcej szczegółów dotyczących rozkładu wykładniczego.
Właściwość bez pamięci
Jedną z najważniejszych właściwości rozkładu wykładniczego jest właściwość bez pamięci: dla dowolnego .
Jest to udowodnione w następujący sposób: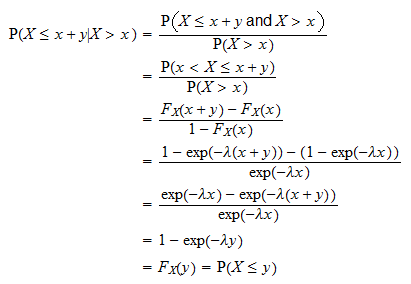 
to czas, w którym musimy czekać przed określonym wydarzeniem występuje. Powyższa właściwość mówi, że prawdopodobieństwo wystąpienia zdarzenia w przedziale czasu o długości jest niezależne od tego, ile czasu już upłynęło () bez zdarzenia.
Suma wykładniczych zmiennych losowych jest zmienną losową Gamma
Załóżmy, że , , …, to niezależne od siebie zmienne losowe o rozkładzie wykładniczym z parametrem .
Zdefiniuj
Następnie suma jest losową zmienną Gamma z parametrami i .
Jest to potwierdzone za pomocą momentu funkcje generujące (pamiętaj, że funkcja generująca moment sumy wzajemnie niezależnych zmiennych losowych jest po prostu iloczynem ich funkcji generujących momenty): Ta ostatnia jest funkcją generującą moment gammy dystrybucja z parametrami i . Więc ma rozkład Gamma, ponieważ dwie zmienne losowe mają ten sam rozkład, gdy mają tę samą funkcję generującą moment.
Czasami mówi się, że zmienna losowa ma rozkład Erlanga. Rozkład Erlanga to tylko szczególny przypadek rozkładu Gamma: zmienna losowa Gamma jest również zmienną losową Erlanga, gdy można ją zapisać jako sumę wykładniczych zmiennych losowych.
Wykres gęstości
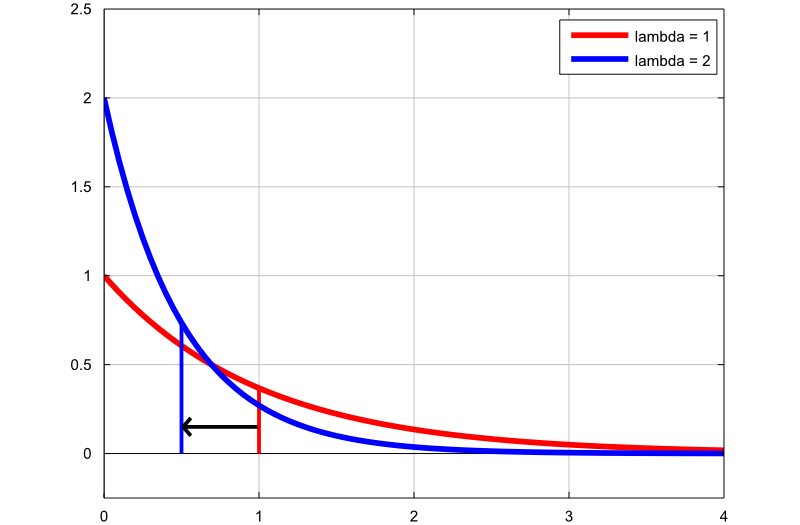
Następny wykres pokazuje, jak zmienia się gęstość rozkładu wykładniczego przez zmianę parametru szybkości:
-
pierwszy wykres (czerwona linia) to funkcja gęstości prawdopodobieństwa wykładniczej zmiennej losowej z parametrem szybkości
; -
Drugi wykres (niebieska linia) to funkcja gęstości prawdopodobieństwa wykładniczej zmiennej losowej z parametrem szybkości
.
Cienkie pionowe linie wskazują średnie z dwóch rozkładów. Zwróć uwagę, że zwiększając parametr szybkości, zmniejszamy średnią rozkładu z do .
Rozwiązane ćwiczenia
Poniżej znajduje się kilka ćwiczeń z wyjaśnionymi rozwiązaniami.
Ćwiczenie 1
Niech będzie wykładniczą zmienną losową z parametrem . Oblicz następujące prawdopodobieństwo:
Przede wszystkim możemy zapisać prawdopodobieństwo jako używając faktu, że prawdopodobieństwo, że ciągła zmienna losowa przyjmie jakąś określoną wartość, jest równe zero (zobacz Ciągłe zmienne losowe i zdarzenia o zerowym prawdopodobieństwie). Teraz prawdopodobieństwo można zapisać w postaci funkcji rozkładu jako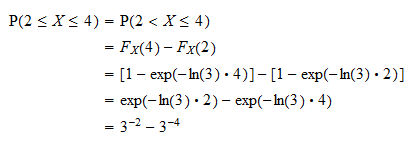 
Ćwiczenie 2
Załóżmy, że zmienna losowa ma rozkład wykładniczy z parametrem . Oblicz następujące prawdopodobieństwo:
To prawdopodobieństwo można łatwo obliczyć za pomocą funkcji rozkładu :
Ćwiczenie 3
Jakie jest prawdopodobieństwo, że zmienna losowa jest mniejsza od oczekiwanej, jeśli ma rozkład wykładniczy z parametrem ?
Oczekiwana wartość wykładniczej zmiennej losowej z parametrem to Powyższe prawdopodobieństwo można obliczyć za pomocą funkcji rozkładu :
Jak cytować
Cytuj jako: