Pomiar: Odkrywanie formuł dla obszaru

Formuły obszarowe

Uczniowie, którzy mają nieformalne pojęcie, że obszar jest „kwotą 2-w” „rzeczy” ”zawarte w regionie mogą wymyślić dla siebie większość formuł, o których zapamiętanie są często proszeni. Każda formuła, którą wymyślają na nowo, wzmacnia ich zrozumienie (i pamięć) dla innych formuł, które znają. (Zobacz także pole powierzchni).

Pole prostokątów

Wybierając kwadrat jako jednostkę pola, uzyskujemy intuicyjne pojęcie o polu prostokątów. Jeśli zdecydujemy, że pole tego kwadratu wynosi 1, wówczas prostokąt 7 razy dłuższy będzie miał 7 × 1 jako jego obszar.

Prostokąt, który jest dwa razy większy od , miałby dwukrotnie większą powierzchnię, więc obszar to 2 × 7 jednostek powierzchni. Możemy policzyć dwa rzędy po siedem kwadratów. Podobnie ma 3 rzędy po 7 kwadratów (lub 7 kolumn po 3 kwadraty), co daje w sumie 7 × 3 kwadratów, więc jego powierzchnia wynosi 21 jednostek kwadratowych.

Liczba kwadratów w jednym rzędzie to długość prostokąta. Liczba rzędów to wysokość prostokąta. A więc pole to długość × wysokość.

Ponieważ prostokąt można narysować pod kątem, „wysokość” jest definiowana jako „kierunek prostopadły do podstawy”, a „podstawa” jest definiowana jako: cóż, bez względu na to, jaką stronę wybierzesz.

To działa w przypadku liczenia liczb. Działa nawet w przypadku ułamków. 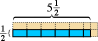Pokazany tutaj niebieski prostokąt ma połowę długość-jednostka wysoka na pięć i pół jednostki długości szerokości. Jeśli wybierzemy odpowiedni kwadrat jako jednostkę powierzchni, zobaczymy, że niebieski prostokąt zawiera pięć połówek powierzchni i jedną czwartą jednostki powierzchni, lub łącznie dwie i trzy czwarte jednostki powierzchni. (Różowe części pokazują zakończenie każdej kwadratowej jednostki powierzchni).

Aby uwzględnić wszystkie liczby, definiujemy obszar prostokąta jako podstawa × wysokość (gdzie „podstawa” i „wysokość” oznaczają długości tych boków mierzone w tych samych jednostkach).

Pole równoległoboków

Zrozumieć

Możemy obliczyć wzór na pole powierzchni równoległoboku przez rozcięcie ułożenie równoległoboku i przestawienie części w celu utworzenia prostokąta. Ponieważ równoległobok i prostokąt składają się z tych samych części, z konieczności mają ten sam obszar. (Zobacz definicję obszaru, aby dowiedzieć się więcej o tym, dlaczego te obszary są takie same).

Widzimy, że mają one również dokładnie tej samej długości podstawy (niebieski) i dokładnie tej samej wysokości (zielony). Ponieważ podstawa × wysokość daje pole prostokąta, możemy użyć tych samych pomiarów na równoległoboku, aby obliczyć jego pole: podstawa × wysokość. (Tak jak poprzednio, „wysokość” jest mierzona prostopadle do podstawy, a „podstawa” jest tą stroną, którą wybrałeś jako pierwsza. Zobacz równoległobok.)

Cięcie pokazane powyżej ułatwia stwierdzenie, że długość podstawy jest niezmieniony. W rzeczywistości prostopadłe cięcie można wykonać w dowolnym miejscu wzdłuż podstawy.

Podparcie otworów

Intuicja i dowód

Ten rozdział daje intuicyjne zrozumienie wzoru pola powierzchni dla równoległoboku, powód, dla którego powinien być tym, czym jest. Ale nie kwestionowaliśmy, czy sekcja rzeczywiście „działa”. Oznacza to, że kiedy wycinamy równoległobok i zmieniamy jego części, spodziewamy się otrzymać , a wynik z pewnością wygląda tak. pozory mogą być mylące. Co zapewnia nas, że kiedy przesuwamy ten trójkąt, wynikiem jest prostokąt? A jeśli bardziej przypomina (choć mniej przesadnie)? Jeśli wynik nie jest zawsze idealny prostokąt, nie możemy wykorzystać naszej wiedzy o wzorze pola prostokąta do opracowania wzoru na równoległobok. W liceum uczniowie będą w stanie udowodnić, że dwie części równoległoboku, po poprawnym złożeniu, tworzą prostokąt . W klasach K-8 w większości uczniowie muszą polegać na wizualnym eksperymencie i intuicyjnie. Dowiedz się więcej o tym, dlaczego te sekcje działają.

A jeśli jako podstawę wybierzemy krótki bok?

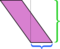
Możemy wybrać dowolny bok jako podstawę; „wysokość” jest zdefiniowany jako mierzone prostopadle do boku, który wybieramy jako podstawę. Jeśli jako podstawę weźmiemy krótszy bok (niebieski), pokazany powyżej podział nie jest tak przekonujący. Cięcie na tej wysokości i przestawianie części pozostawia bałagan:

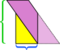
W tym konkretnym przykładzie możemy uratować bałagan, wykonując jeszcze jedno cięcie, 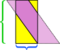, ale co by było, gdyby równoległobok był jeszcze dłuższy i węższy?

Okazuje się, że każdy równoległobok, nieważne jak długi i chudy, może zostać rozcięty w ten sposób, aby części – być może wiele z nich – można było ułożyć w prostokąt. Ale potrzeba więcej pracy, aby pokazać, że zawsze można to zrobić. Potrzebujemy innego pomysłu.

Nieco inny pomysł na sekcję znacznie ułatwia życie w tym przypadku. (Samodzielnie możesz pokazać, że działa to również w oryginalnym przypadku.)

• Zamknij równoległobok w prostokącie.
• Dwie części prostokąta, które nie znajdują się wewnątrz równoległoboku, to przystające trójkąty.
• Przesuń jeden z tych trójkątów w kierunku drugiego, aż spotkają się, tworząc prostokąt. 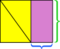Ponieważ całkowity obszar zewnętrznego prostokąta nie zmienił się (jest to ten sam prostokąt co poprzednio), a żółty obszar nie zmienił się (elementy po prostu się przesunęły), różnica między one – fioletowe obszary – muszą być takie same. Tak jak poprzednio, możemy również zobaczyć, że wymiary prostokątnego fioletowego obszaru są podstawą i wysokością oryginalnego równoległoboku.

Intuicja i dowód, powtórzenie : Ponownie, rozwarstwienie zapewnia niezbędny wgląd, ale potrzeba trochę więcej pracy, aby upewnić się, że dwa żółte trójkąty, które z pewnością wyglądają tak, jakby pasowały do siebie, tworząc prostokąt, naprawdę pasują dokładnie, a nie tylko prawie.

Dlaczego tak ważne jest, aby być tak ostrożnym?

Kiedy tworzymy inne formuły na pole (poniżej), będziemy chcieli skorzystać z naszego sposobu, jak znaleźć pole równoległoboku, więc chcemy aby móc polegać na znalezionej przez nas regule. Możemy być pewni, że przestawianie części nie zmienia obszaru: czyli w końcu to, jak definiujemy obszar. Ale musimy też mieć pewność, że części pasują do siebie tak, jak twierdzimy, lub nie możemy polegać na pomiarach, które wykonaliśmy. I musimy być pewni, że zasada podstawa × wysokość nie zależy od szczęśliwego wyboru podstawy.

W większości programów nauczania uczniowie nie mają wystarczająco systematycznej podstawy wiedzy geometrycznej przed klasą 8, aby dźwiękowe dowody, że te sekcje działają. Ale intuicyjne zrozumienie wystarczy, aby wyjaśnić i uzasadnić wzory, i stanowi dobrą podstawę do późniejszych badań geometrycznych.

Obszar trójkąta

Znajomość tego, jak znaleźć pole równoległoboku, pomaga nam znajdź pole trójkąta.

Cięcie trójkąta

Możemy podzielić trójkąt na dwie części – jedną z nich na trójkąt, a drugą na trapez – przecinając go równolegle do podstawy. Jeśli przecinamy wysokość dokładnie o połowę za pomocą tego kawałka, dwie części pasują do siebie, tworząc równoległobok o tej samej podstawie, ale o połowie wysokości.

Zatem podstawa × połowa wysokości daje pole trójkąta. Podobny podział pokazuje połowę podstawy x wysokość. Każde z nich redukuje się do bh.

Podwojenie trójkąta, a następnie podzielenie na pół wynikowego obszaru

Inny sposób myślenia: dwie kopie trójkąt tworzy równoległobok o tej samej podstawie i wysokości co trójkąt.

Pole równoległoboku to podstawa × wysokość, ale to jest dwa razy większe od pola trójkąta, więc obszar trójkąta to podstawa × wysokość, jak widzieliśmy w metodzie podziału.

(Jak zawsze , wybierz „podstawę” i zmierz wysokość prostopadłą do tej podstawy, od podstawy do przeciwległego wierzchołka.)

Pole trapezu

Podwojenie trapezu, a następnie podzielenie uzyskanego obszaru na pół

Tak jak w przypadku trójkąta, dwie kopie trapezu można dopasować razem, tworząc równoległobok.

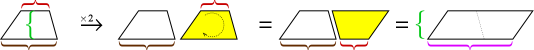
Wysokość równoległoboku jest taka sama jak wysokość trapezu, ale jego podstawa jest sumą dwóch podstaw trapezu. Zatem powierzchnia równoległoboku to wysokość × (podstawa1 + podstawa2). Ale ten obszar to dwa trapezoidy, więc musimy go przeciąć na pół, aby uzyskać obszar trapezu.

Wycinanie trapezu

Możemy również wypreparować trapez tak, jak dokonaliśmy sekcji trójkąt, z pojedynczym kawałkiem przecinającym jego wysokość o połowę. Te dwie części pasują do siebie, tworząc równoległobok, którego podstawa jest sumą dwóch podstaw trapezu, ale którego wysokość jest równa połowie wysokości trapezu.

W przypadku trapezu podstawy nie mogą być wybieranym do woli. Dwa równoległe boki to podstawy, a wysokość, jak zawsze, jest prostopadłą odległością od jednej podstawy do przeciwnej.

Pole tego równoległoboku to jego wysokość (połowa wysokości trapezu) pomnożona przez jego podstawę (suma podstaw trapezu), więc jego powierzchnia jest równa połowie wysokości × (podstawa1 + podstawa2). Ponieważ równoległobok jest wykonany z dokładnie tego samego „materiału” co trapez, jest to również obszar trapezu.

Tak czy inaczej, obszar trapezu to × wysokość × (podstawa1 + podstawa2).

Obszar innych specjalnych czworoboków

Obszar rombu

Obszar rombu można znaleźć, przecinając i przestawiając elementy tak, aby utworzyły równoległobok. Można to zrobić na kilka sposobów:

1. Przeciąć krótszą przekątną (a), aby utworzyć dwa przystające trójkąty. Przesuń dolną połowę trójkąta obok górnej, aby utworzyć równoległobok. Krótsza przekątna (a) staje się podstawą równoległoboku, a połowa dłuższej przekątnej (b) staje się wysokością równoległoboku. Zatem obszar rombu jest * b lub iloczynem przekątnych, co jest standardową formułą dla rombu.
2. Innym podobnym sposobem jest pocięcie rombów na cztery przystające trójkąty i przestawienie ich w prostokąt z krótszą przekątną jako podstawą i połową dłuższą przekątną jako wysokością.
3. Po przecięciu romb na dwa przystające trójkąty, możemy obliczyć pole jednego z trójkątów, które wynosi * podstawa (a) * wysokość ( b) = ab. Następnie pomnóż przez dwa, ponieważ jest ich dwa: 2 * ab = ab.

Powierzchnia latawca

Powierzchnia latawca może być podobna do obszaru rombu. Cięcie w poprzek dłuższej przekątnej daje dwa przystające trójkąty. Jeśli je przestawimy, możemy utworzyć równoległobok z dłuższą przekątną (b) jako podstawą i połową krótszą przekątną (a) jako wysokością. Zatem obszar staje się b * a = ab. Bardziej skomplikowane podejście wymaga trochę algebry. Przetnij latawiec w poprzek krótszej przekątnej, aby utworzyć dwa trójkąty z krótszą przekątną (a) jako podstawą. Zatem obszar pierwszego trójkąta to a * faliste, gdzie faliste to wysokość. Obszar drugiego trójkąta to a * (b – faliste), gdzie (b – faliste) to pozostała część dłuższej przekątnej. W ten sposób całkowity obszar staje się ( a * squiggly) + ( a * (b – squiggly)). Biorąc pod uwagę a, mamy a (squiggly + b – squiggly) = ab.

Cóż, co wiesz. Zasadniczo wystarczy znać wzór na pole powierzchni równoległoboku, a następnie wyprowadzić wzór na pozostałe.