Jak obliczyć powierzchnię

Obliczanie powierzchni

Powierzchnia jest mierzona w kwadratach (lub jednostkach kwadratowych).

Ile kwadratów znajduje się w tym prostokącie?

Możemy policzyć kwadraty lub weź długość i szerokość i użyj mnożenia. Powyższy prostokąt ma powierzchnię 15 jednostek kwadratowych.

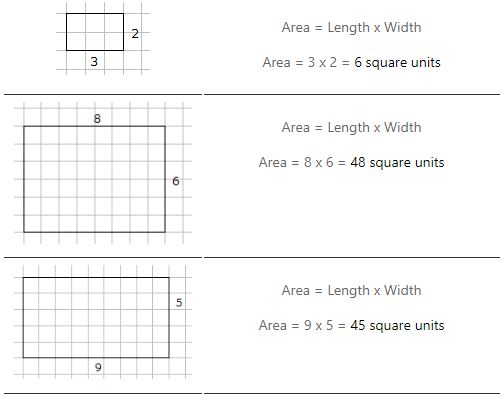
Pole prostokąta to = długość x szerokość

Przykłady obliczania pola powierzchni prostokąta

Jednostki do pomiaru powierzchni

Mierzymy powierzchnię za pomocą kwadratów. Używamy różnych rozmiarów kwadratów w zależności od tego, jak duży lub mały jest obszar.

Przykład	Długość boku na kwadratach	Jednostka
Rozmiar paznokieć w kciuku	Milimetr	mm2
Rozmiar kartki papieru	Centymetr	cm2
Rozmiar pomieszczenia	Metr	m2
Wielkość miasta	Kilometr	km2

Nie zapomnij o małym 2

Piszemy rozmiary kwadratów, używając małych 2 obok jednostki.
Piszemy mm2, cm2, m2, km2, cm2
Możemy powiedzieć „63 milimetry do kwadratu” lub „63 milimetry kwadratowe”

Moglibyśmy użyć małych kwadratów do pomiaru dużych powierzchni. Jedynym problemem jest to, że musielibyśmy użyć bardzo dużych liczby. Na przykład pole może być mierzone na 5 000 000 000 milimetrów kwadratowych, podczas gdy rozmiar 5 000 metrów kwadratowych byłby dużo łatwiejszy do powiedzenia, napisania i wizualizacji.

Prawdopodobnie usłyszysz więcej jednostek pomiaru powierzchni; cale kwadratowe, stopy kwadratowe, jardy kwadratowe, mile kwadratowe, akry, hektary to wszystkie jednostki używane do pomiaru powierzchni.

Więcej przykładów obliczania powierzchni

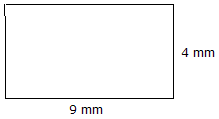	Obszar = długość x szerokość Obszar = 9 mm x 4 mm = 36 mm2
	Powierzchnia = długość x szerokość Powierzchnia = 7 cm x 6 cm = 42 cm2
	Powierzchnia = Długość x Szerokość Powierzchnia = 8 mx 2 m = 16 m2
	Powierzchnia = długość x szerokość Powierzchnia = 7 km x 5 km = 35 km2

Pole kwadratu

Długość i szerokość kwadratu są takie same, więc wystarczy pomnożyć długość przez długość.

Powierzchnia = długość x długość Powierzchnia = 6 cm x 6 cm = 36 cm2

Obszar koła

Obszar koła = πr2
gdzie r jest promieniem okręgu, a π jest stosunkiem obwodu koła do jego średnicy.

π (wymawiane jako „ciasto” i często zapisywane jako „Pi”) jest nieskończoną liczbą dziesiętną ze wspólnym przybliżenie 3.14159. Więcej informacji o Pi znajdziesz tutaj

Przykład obliczania pola koła

Obszar = πr2 Obszar = 3,14159 x (4 cm) 2 Powierzchnia = 3,14159 x 16 cm2 Powierzchnia = 50,27 cm2 Odpowiedź zaokrąglona do 2 miejsc po przecinku

Objaśnienie obszaru wzoru koła

Weź okrąg i podziel go na sektory o jednakowej wielkości i przestaw je, jak pokazano poniżej. Zauważ, że gdy sektory stają się mniejsze, kształt staje się bardziej podobny do prostokąta. Uwaga: Nie ma ograniczeń co do tego, jak małe mogą być te sektory i jak blisko mogą przypominać prostokąt po ułożeniu.

Zakładając, że wiemy, że obwód koła jest równy 2πr, możemy dodać wymiary do „prostokąt”, jak pokazano poniżej. Używając pola powierzchni prostokąta, obszar = szerokość x wysokość, możemy zobaczyć, jak nasz okrąg, ponownie skonfigurowany jako prostokąt, może mieć obszar zbliżony do πr xr lub πr2

Okrąg Przegrupowanie sektorów

Przekształcenie sektorów okręgu – rozpoczęcie wyglądać jak prostokąt

Obszar Kształty złożone

Istnieje wiele przypadków, w których obliczenie całkowitej powierzchni wymaga obliczenia więcej niż jednego obszaru, po którym następuje dodawanie, odejmowanie lub inna kombinacja operacji w celu znalezienia wymaganej powierzchni.

Uwaga: W poniższych przykładach jednostki miary nie są pokazane, a odpowiedzi i wartość π (Pi) zostały zaokrąglone do najbliższej setnej.

Przykład: Proste złożone kształty

Poniższy przykład obliczenia powierzchni jest stosunkowo prosty. Kształt można zobaczyć jako trójkąt połączony z prostokątem.

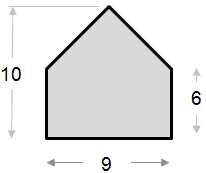Obszar części trójkąta: ½ x podstawa x wysokość ½ x 9 x 4 = 18 Powierzchnia części prostokąta: szerokość x wysokość 9 x 6 = 54 Powierzchnia całkowita = 18 + 54 = 72

Powyższy przykład ilustruje typowe wymagania podczas pracy ze złożonymi kształty – znajdowanie wymiarów, które nie są pokazane. Udzielając korepetycji swoim dzieciom, w razie potrzeby pomagaj znaleźć te „brakujące” wymiary. Poniżej znajduje się inny przykład.

Znajdowanie wymiarów

Jakie są wymiary małej prostokątnej części? Szerokość? 12 – 7 – 2 = 3 Wysokość? 8 – 6 = 2

Przykład: odejmowanie jednego obszaru od drugiego

W poniższym przykładzie kształt można zobaczyć jako prostokąt z wyciętym trójkątem.

Pole części prostokąta: szerokość x wysokość 5 x 6 = 30 Pole części trójkąta: ½ x podstawa x wysokość ½ x 3 x 3 = 4,50 Powierzchnia całkowita = 30 – 4,50 = 25,50

Przykład: częściowe obszary

Poniższy przykład jest podobny do powyższego, chociaż ponieważ mamy półkole, musimy obliczyć ułamek (połowę) obszaru koła. Zwróć uwagę, że w tym przykładzie pokazano średnicę, a nie promień.

Pole części trójkąta: ½ x podstawa x wysokość ½ x 6 x 6 = 18 Pole części półkola: ½ x (πr2) ½ x (3,14 x 1,52) = 3,53 Całkowita powierzchnia = 18 – 3,53 = 14,47

Przykład: decyzje! Połączyć? Odejmowanie

Powszechnie jest więcej niż jeden sposób obliczenia końcowego pola. W poniższych przykładach kształt można zobaczyć jako dwa połączone prostokąty lub jako jeden duży prostokąt z mniejszym prostokątem „wyciętym” z prawego górnego rogu.

Arkusze obliczania powierzchni

Drukuj Wypełnij poniższe arkusze i wykorzystaj je do ćwiczeń podczas nauczania swoich dzieci.

• Obliczanie obszarów – prostokąty i kwadraty
• Obliczanie obszarów – prostokąty
• Obliczanie Obszary – prostokąty
• Obliczanie powierzchni złożonych np o prostokątnych kształtach
• Obliczanie obszarów złożonych, np. z prostokątami, trójkątami i okręgami
• Obliczanie obszarów, np. trójkątów
• Pole koła
• Obliczanie powierzchni np. prostokątnych pryzmatów

Znajdziesz tutaj więcej arkuszy geometrii do wydrukowania.