Jak obliczyć objętość

Obliczanie objętości

Objętość mierzy się w kostkach (lub jednostkach sześciennych).

Ile sześcianów znajduje się w tym prostokątnym pryzmacie (prostopadłościanie)?

Możemy policzyć kostki, chociaż szybciej jest wziąć długość, szerokość i wysokość i użyć mnożenia. Powyższy prostokątny pryzmat ma objętość 48 jednostek sześciennych.

Objętość prostokąta wynosi = długość x szerokość x wysokość

Przykłady obliczania pola powierzchni prostokąta

Aby obliczyć objętość, musimy wykonać dwa mnożenia. Obliczamy powierzchnię jednej twarzy (lub boku) i mnożymy ją przez jej wysokość. Poniższe przykłady pokazują, jak można to zrobić na trzy sposoby.

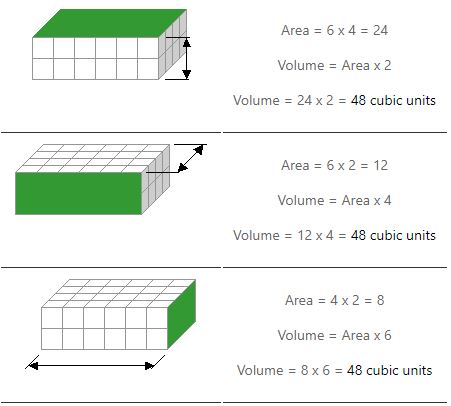
Zwróć uwagę, jak otrzymujemy tę samą odpowiedź bez względu na to, której strony użyjemy do znalezienia obszaru.

Kiedy Twoje dziecko zaczyna pracować z obszarem i obwodem, zwykle pracuje z dwoma wymiarami – kwadraty, prostokąty, trójkąty itp., które są pokazane na papierze jako płaskie – nie ma głębokości ani trzeciego wymiaru. Praca z objętością obejmuje 3 wymiary. Upewnij się, że Twoje dziecko jest tego świadome i nie myśli o kostkach i innych kształtach 3D pokazanych na papierze jako po prostu o kolejnym „kształcie na stronie”. Pokaż im prawdziwe pudełka i pokaż, jak można je narysować (lub przedstawić) na dwuwymiarowej kartce papieru. Innymi słowy, upewnij się, że połączenie między tym, co jest na papierze, a tym, co reprezentuje w prawdziwym świecie, zostało stworzone.

Upewnij się, że Twoje dziecko nie jest zdezorientowane użyciem głośności używanej podczas mówienia o głośności .

Jednostki pomiaru objętości

Istnieją bardzo duże różnice między jednostkami miary objętości. Na przykład jest 100 centymetrów na 1 metr, ale jest 1 000 000 (tak, 1 milion ) centymetrów sześciennych w metrze sześciennym.

Skąd ta duża różnica? Ponieważ w objętości mamy nie tylko długość, mamy długość, szerokość i wysokość. Pokazuje to poniższy przykład kostki cukru.

Ile cukru? 1 m3 lub 1 000 000 cm3

Pomyśl o napełnieniu bardzo dużego pudełka (miałoby ono 1 metr szerokości, 1 metra długości i 1 metra wysokości) kostkami cukru (z każdą bok 1 centymetr).

	Krok 1: jeden wiersz u dołu pola – to będzie 100 kostki cukru
	Krok 2: zakryj pozostałą część podstawy pudełka – co dałoby w sumie 100 wierszy każdy z 100 kostek cukru. 100 x 100 = 10000 kostek cukru kostek na dole dużego pudełka.
	Krok 3: Powtórz to 99 razy, aż będzie warstwy po 10 000 kostek ułożone na 100 głębokich warstw. 10 000 x 100 = 1 000 000 kostek cukru

1 m3 ma 1 000 000 cm3 – uważaj, aby nie mieć za dużo cukru!

Istnieją inne jednostki pomiaru objętości; cale sześcienne, stopy sześcienne, jardy sześcienne to wszystkie jednostki używane do pomiaru objętości. Mililitry, litry, galony są również używane, szczególnie do pomiaru cieczy.

Nie zapomnij o kropce 3

Piszemy rozmiary sześcienne za pomocą małej 3 obok jednostki.
Piszemy mm3, cm3, m3, km3, cm3
Możemy powiedzieć „85 centymetrów sześciennych” lub „85 centymetrów sześciennych”

Przykłady obliczania objętości pryzmatów prostokątnych

	Objętość = długość x szerokość x wysokość Objętość = 12 cm x 8 cm x 6 cm = 576 cm3
	Objętość = długość x szerokość x wysokość Objętość = 20 mx 2 mx 2 m = 80 m3
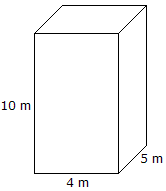	Objętość = długość x szerokość x Wysokość Objętość = 10 mx 4 mx 5 m = 200 m3

Objętość cylindra

Obliczanie objętości cylindra der polega na pomnożeniu powierzchni podstawy przez wysokość cylindra. Podstawa walca jest okrągła, a wzór na pole koła to: pole koła = πr2. W obszarze koła jest więcej.

Objętość = powierzchnia podstawy x wysokość Objętość = πr2 xh Objętość = πr2 h

Uwaga: w poniższych przykładach użyjemy 3,14 jako przybliżonej wartości dla π (Pi).

Przykład obliczenia objętości cylindra

Wymiary podano w cm.

Objętość = πr2 h Objętość = 3.14 x 3 x 3 x 8 Objętość = 226,08 cm3

Objętość stożka

Objętość stożka jest równa jednej trzeciej objętości walca o dopasowanej wysokości i powierzchni podstawy. Daje to wzór na objętość stożka, jak pokazano poniżej.

Tom = 1/3 πr2h

Przykład obliczania objętości stożka

Wymiary w cm.

Objętość = 1/3 πr2 h Objętość = 1/3 x 3,14 x 2 x 2 x 7 Objętość = 29,31 cm3

Objętość kuli

Wzór na objętość kuli przedstawiono poniżej.

Tom = 4/3 πr3

Przykład obliczania objętości kuli

Wymiary podano w cm.

Objętość = 4/3 πr3 Objętość = 4/3 x 3,14 x 4 x 4 x 4 Objętość = 267,95 cm3

Arkusze objętości do druku

Użyj poniższego arkusza, aby przećwiczyć obliczanie objętości.

• Znajdowanie objętości w jednostkach sześciennych – prostokątne graniastosłupy i kompozyty
• Objętości pryzmatów prostokątnych
• Objętości pryzmatów prostokątnych
• Objętości obiektów ze świata rzeczywistego, np. pudełek płatków śniadaniowych
• Obliczanie objętości, np. trójkątnych pryzmatów i cylindrów

Otrzymasz tutaj inne arkusze geometrii na temat obwodu, obszaru i nie tylko.