Dystrybucja Poissona
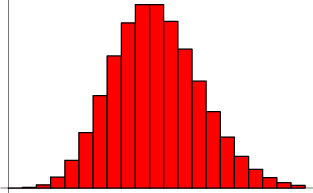
Biorąc pod uwagę proces Poissona, prawdopodobieństwo uzyskania dokładnie ![]() sukcesów w
sukcesów w ![]() próbach jest określone przez granicę rozkładu dwumianowego
próbach jest określone przez granicę rozkładu dwumianowego
| |
(1)
|
Wyświetlanie rozkładu jako funkcji oczekiwanej liczby sukcesów
| |
(2)
|
zamiast rozmiaru próbki ![]() dla ustalonego
dla ustalonego ![]() , równanie (2) staje się
, równanie (2) staje się
| |
(3)
|
Jeśli rozmiar próbki ![]() stanie się duży, dystrybucja zbliża się do
stanie się duży, dystrybucja zbliża się do
| |
|
|
(4)
|
| |
|
|
(5)
|
| |
|
|
(6)
|
| |
|
|
(7)
|
| |
|
|
(8)
|
znany jako rozkład Poissona (Papoulis 1984, str. 101 i 554; Pfeiffer i Schum 1973, s. 200). Zwróć uwagę, że wielkość próby ![]() całkowicie wypadła z funkcji prawdopodobieństwa, która ma taką samą postać funkcjonalną dla wszystkich wartości
całkowicie wypadła z funkcji prawdopodobieństwa, która ma taką samą postać funkcjonalną dla wszystkich wartości ![]() .
.
Rozkład Poissona jest zaimplementowany w języku WolframLanguage jako PoissonaDistribution.
Zgodnie z oczekiwaniami rozkład Poissona jest znormalizowany, tak że suma prawdopodobieństw jest równa 1, ponieważ
| |
(9 )
|
Współczynnik prawdopodobieństw jest określony wzorem
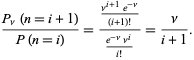 |
(10)
|
Rozkład Poissona osiąga maksimum, gdy
| |
(11)
|
gdzie to stała Eulera-Mascheroniego, a ![]() to liczba harmoniczna prowadząca do równania transcendentalnego.
to liczba harmoniczna prowadząca do równania transcendentalnego.
| |
(12)
|
, którego nie można dokładnie rozwiązać dla ![]() .
.
Funkcja generująca momenty rozkładu Poissona jest określona wzorem
| |
|
|
(13)
|
| |
|
|
(14)
|
| |
|
|
(15)
|
| |
|
|
(16)
|
| |
|
|
(17)
|
| |
|
|
(18)
|
więc
| |
|
|
(19)
|
| |
|
|
(20)
|
(Papoulis 1984, s. 554).
Nieprzetworzone momenty można również obliczyć bezpośrednio poprzez sumowanie, co daje nieoczekiwane połączenie z wielomianem Bella ![]() i liczbami Stirlinga drugiego rodzaju,
i liczbami Stirlinga drugiego rodzaju,
| |
(21)
|
znany jako formuła Dobińskiego.Dlatego
| |
|
|
(22)
|
| |
|
|
(23)
|
| |
|
|
(24)
|
Centralne momenty można następnie obliczyć jako
| |
|
(25)
|
|
| |
|
|
(26)
|
| |
|
|
(27)
|
więc średnia, wariancja, skośność i nadmiar kurtozy wynoszą
| |
|
|
(28)
|
| |
|
|
(29)
|
| |
|
|
(30)
|
| |
|
|
(31)
|
| |
|
|
(32)
|
Charakterystyczną funkcją Poissondistribution jest
(Papoulis 1984, str. 154 i 554), a funkcją generującą kumulację jest
| |
(34)
|
więc
| |
(35)
|
Średnie odchylenie rozkładu Poissona jest określone przez
| |
(36)
|
Rozkład Poissona można również wyrazić jako
| |
(37)
|
| |
(38)
|
Funkcja generująca momenty rozkładu Poissona w dwóch zmiennych jest określona wzorem
| |
(39)
|
Jeśli zmienne niezależne ![]() ,
, ![]() , …,
, …, ![]() mają rozkłady Poissona z parametrami
mają rozkłady Poissona z parametrami ![]() ,
, ![]() , …,
, …, ![]() , a następnie
, a następnie
| |
(40)
|
ma rozkład Poissona z parametrem
| |
(41)
|
Widać to, ponieważ funkcją generującą kumulację jest
| |
(42)
|
| |
(43)
|
Uogólnienie rozkładu Poissona zostało użyte przez Sasława (1989) do modelowania obserwowane gromady galaktyk we Wszechświecie. Formę tej dystrybucji określa
| |
(44)
|
gdzie ![]() to liczba galaktyk w objętości
to liczba galaktyk w objętości ![]() ,
, ![]() ,
, ![]() to średnia gęstość galaktyk, a
to średnia gęstość galaktyk, a ![]() , gdzie
, gdzie ![]() to stosunek energii grawitacyjnej do kinetyki energia dziwnych ruchów, Pozwalanie
to stosunek energii grawitacyjnej do kinetyki energia dziwnych ruchów, Pozwalanie ![]() daje
daje
| |
(45)
|
co jest rzeczywiście rozkładem Poissona z ![]() . Podobnie, zezwolenie na
. Podobnie, zezwolenie na ![]() daje
daje ![]() .
.