College Algebra (Polski)
Wyniki nauczania
- Zidentyfikuj wierzchołek, oś symetrii, punkt przecięcia z osią Y oraz minimalną lub maksymalną wartość paraboli na podstawie to jest wykres.
- Zidentyfikuj funkcję kwadratową zapisaną w formie ogólnej i wierzchołkowej.
- Biorąc pod uwagę funkcję kwadratową w formie ogólnej, znajdź wierzchołek.
- Zdefiniuj dziedzinę i zakres funkcji kwadratowej poprzez zidentyfikowanie wierzchołka jako maksimum lub minimum.
Wykres funkcji kwadratowej jest krzywą w kształcie litery U zwaną parabolą. Jedną z ważnych cech wykresu jest to, że ma on skrajny punkt, zwany wierzchołkiem. Jeśli parabola się otwiera, wierzchołek reprezentuje najniższy punkt na wykresie lub minimalną wartość funkcji kwadratowej. Jeśli parabola otwiera się w dół, wierzchołek reprezentuje najwyższy punkt na wykresie lub wartość maksymalną. W obu przypadkach wierzchołek jest punktem zwrotnym na wykresie. Wykres jest również symetryczny z pionową linią poprowadzoną przez wierzchołek, zwaną osią symetrii.
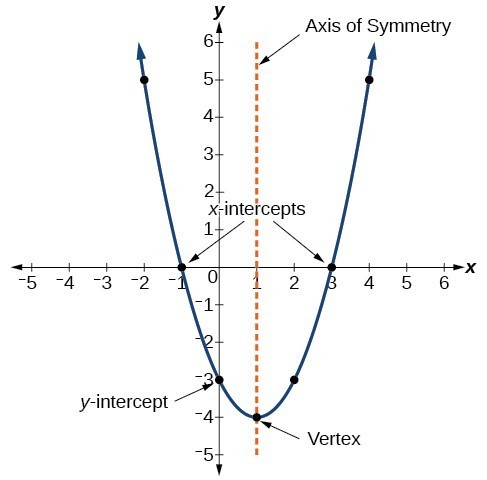
Równania funkcji kwadratowych
Ogólna postać funkcji kwadratowej przedstawia funkcję w postaci
f \ left (x \ right) = a {x} ^ {2} + bx + c
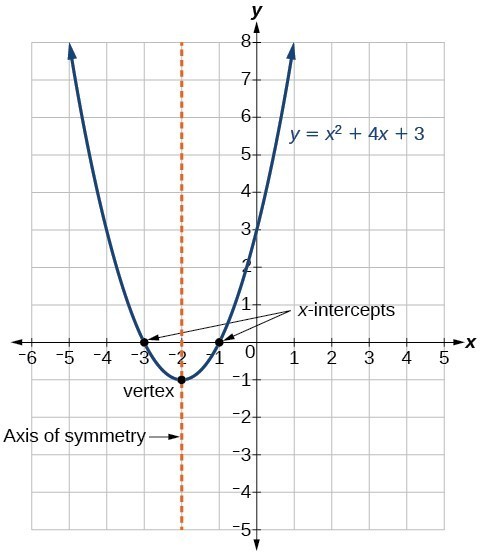
Standardowa postać funkcji kwadratowej przedstawia funkcję w postaci
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Biorąc pod uwagę ogólnie funkcję kwadratową form, znajdź wierzchołek paraboli.
Jednym z powodów, dla których możemy chcieć zidentyfikować wierzchołek paraboli jest to, że ten punkt poinformuje nas, gdzie występuje maksymalna lub minimalna wartość wyjścia, k i gdzie zdarza się, h. Jeśli otrzymamy ogólną postać funkcji kwadratowej:
f (x) = ax ^ 2 + bx + c
Możemy zdefiniować wierzchołek (h, k), wykonując następujące czynności:
Znajdowanie dziedziny i zakresu funkcji kwadratowej
Wartość wejściową funkcji kwadratowej może być dowolna liczba. Dlatego dziedziną dowolnej funkcji kwadratowej są wszystkie liczby rzeczywiste. Ponieważ parabole mają maksimum lub minimum na wierzchołku, zasięg jest ograniczony. Ponieważ wierzchołek paraboli będzie maksymalny lub minimalny, zakres będzie składał się ze wszystkich wartości y większych lub równych współrzędnej y wierzchołka lub mniejszych lub równych współrzędnej y w punkcie zwrotnym , w zależności od tego, czy parabola otwiera się, czy opuszcza.
Wnieś wkład!
Ulepsz tę stronęDowiedz się więcej