Zidentyfikuj asymptoty pionowe i poziome | College Algebra

8 listopada, 2020

College Algebra (Polski)

Patrząc na wykres funkcji wymiernej, możemy zbadać jej lokalne zachowanie i łatwo sprawdzić, czy istnieją asymptoty. Możemy nawet w przybliżeniu określić ich lokalizację. Jednak nawet bez wykresu nadal możemy określić, czy dana funkcja wymierna ma asymptoty i obliczyć ich położenie.

Asymptoty pionowe

Asymptoty pionowe funkcji wymiernej mogą być znalezione przez zbadanie czynników mianownika, które nie są wspólne dla czynników w liczniku. Asymptoty pionowe występują przy zerach takich czynników.

Porada: Mając wymierną funkcję, zidentyfikuj pionowe asymptoty jej wykresu.

Uwzględnij licznik i mianownik.
Zwróć uwagę na wszelkie ograniczenia w dziedzinie funkcji.
Zredukuj wyrażenie, anulując wspólne czynniki w liczniku i mianowniku.
Zanotuj wszystkie wartości które powodują, że mianownik ma wartość zero w tej uproszczonej wersji. To tam występują asymptoty pionowe.
Zwróć uwagę na wszelkie ograniczenia w domenie, w której asymptoty nie występują. Są to usuwalne nieciągłości.

Usuwalne nieciągłości

Czasami wykres zawiera dziurę: pojedynczy punkt, w którym wykres nie jest zdefiniowany, wskazywany przez otwarty krąg. Taką dziurę nazywamy usuwalną nieciągłością.

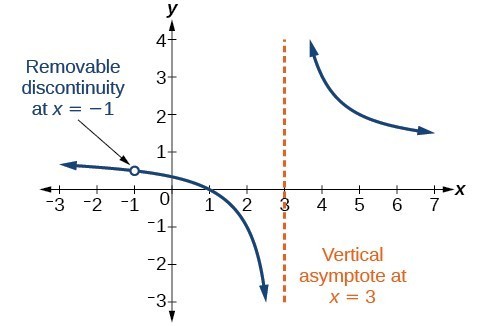
f \ left (x \ right) = \ frac {\ left (x + 1 \ right) \ left (x – 1 \ right)} {\ left (x + 1 \ right) \ left (x – 3 \ right)}

Rysunek 10

Ogólna uwaga: usuwalne nieciągłości funkcji wymiernych

Usuwalna nieciągłość występuje na wykresie funkcji wymiernej przy x = a, jeśli a jest zerem dla czynnika w mianowniku, który jest wspólny z czynnikiem w liczniku. Czynimy licznik i mianownik i sprawdzamy czynniki wspólne. Jeśli jakieś znajdziemy, ustawiamy wspólny współczynnik równy 0 i rozwiązujemy. To jest lokalizacja usuwalnej nieciągłości. Dzieje się tak, jeśli krotność tego czynnika jest większa lub równa tej w mianowniku. Jeśli krotność tego czynnika jest większa w mianowniku, to nadal istnieje asymptota przy tej wartości.

Asymptoty poziome

Podczas gdy asymptoty pionowe opisują zachowanie wykres gdy dane wyjściowe stają się bardzo duże lub bardzo małe, poziome asymptoty pomagają opisać zachowanie wykresu, gdy dane wejściowe stają się bardzo duże lub bardzo małe. Przypomnij sobie, że końcowe zachowanie wielomianu będzie odzwierciedlać zachowanie terminu wiodącego. Podobnie, końcowe zachowanie funkcji wymiernej będzie odzwierciedlać stosunek wiodących składników funkcji licznika i mianownika.

Podczas sprawdzania asymptot poziomych występują trzy różne wyniki:

Przypadek 1: Jeśli stopień mianownika > stopień licznika, występuje pozioma asymptota w miejscu y = 0.

\ text {Przykład:} f \ left (x \ right) = \ frac {4x + 2} {{x} ^ {2} + 4x – 5}

Przypadek 2: Jeśli stopień mianownika < stopień licznika o jeden, otrzymujemy asymptotę skośną.

\ text {Przykład:} f \ left (x \ right) = \ frac {3 {x} ^ {2} -2x + 1} {x – 1}

\ text {Przykład:} f \ left (x \ right) = \ frac {3 {x} ^ {2} +2} {{x} ^ {2 } + 4x – 5}

Zauważ, że chociaż wykres funkcji wymiernej nigdy nie przecina pionowej asymptoty, wykres może, ale nie musi, przecinać poziomy lub asymptota skośna. Ponadto, chociaż wykres funkcji wymiernej może mieć wiele asymptot pionowych, wykres będzie miał co najwyżej jedną asymptotę poziomą (lub skośną).

Należy zauważyć, że jeśli stopień licznika jest większy niż stopień mianownika o więcej niż jeden, końcowe zachowanie wykresu będzie naśladować zachowanie zredukowanej części zachowania końcowego. Na przykład, gdybyśmy mieli funkcję

f \ left (x \ right) = \ frac {3 {x} ^ {5} – {x} ^ { 2}} {x + 3}

z zachowaniem końcowym

f \ left (x \ right) \ ok \ frac {3 {x } ^ {5}} {x} = 3 {x} ^ {4},

końcowe zachowanie wykresu wyglądałoby podobnie do zachowania parzystego wielomianu z dodatnim współczynnikiem wiodącym.

x \ to \ pm \ infty, f \ left (x \ right) \ to \ infty

Ogólna uwaga: poziome asymptoty Funkcje wymierne

Poziomą asymptotę funkcji wymiernej można określić, patrząc na stopnie licznika i mianownika.

Stopień licznika jest mniejszy niż stopień mianownika: asymptota pozioma przy y = 0.
Stopień licznika jest większy niż stopień mianownika o jeden: brak asymptoty poziomej; asymptota skośna.
Stopień licznika jest równy stopniowi mianownika: asymptota pozioma przy stosunku współczynników wiodących.

Ogólna uwaga: punkty przecięcia funkcji wymiernych

Funkcja wymierna będzie miała punkt przecięcia z osią y, gdy wartość wejściowa wynosi zero, jeśli funkcja jest zdefiniowana na zero. Funkcja wymierna nie będzie miała punktu przecięcia z osią y, jeśli funkcja nie jest zdefiniowana jako zero.

Podobnie funkcja wymierna będzie miała punkty przecięcia z osią x na wejściach, które spowodują, że na wyjściu będzie zero. Ponieważ ułamek jest równy zero tylko wtedy, gdy licznik jest równy zero, przecięcia z osią x mogą wystąpić tylko wtedy, gdy licznik funkcji wymiernej jest równy zero.

Spróbuj 7

Biorąc pod uwagę funkcję odwrotności do kwadratu, która jest przesunięta o 3 jednostki w prawo io 4 jednostki w dół, zapisz ją jako funkcję wymierną. Następnie znajdź punkty przecięcia z osiami x– i y oraz asymptoty poziome i pionowe.

Rozwiązanie

admin