Poisson-distributie
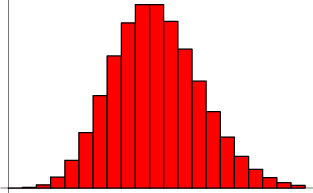
Gegeven een Poisson-proces, wordt de kans om exact ![]() successen te behalen in
successen te behalen in ![]() -proeven gegeven door de limiet van een binominale verdeling
-proeven gegeven door de limiet van een binominale verdeling
| |
(1)
|
De distributie bekijken als een functie van het verwachte aantal successen
| |
(2)
|
in plaats van de steekproefomvang ![]() voor vast
voor vast ![]() , wordt vergelijking (2) dan
, wordt vergelijking (2) dan
| |
(3)
|
Door de steekproefomvang ![]() groot te laten worden, nadert de distributie
groot te laten worden, nadert de distributie
| |
|
|
(4)
|
| |
|
|
(5)
|
| |
|
|
(6)
|
| |
|
|
(7)
|
| |
|
|
(8)
|
die bekend staat als de Poisson-verdeling (Papoulis 1984, pp. 101 en 554; Pfeiffer en Schum 1973, p. 200). Merk op dat de steekproefomvang ![]() volledig is verwijderd uit de waarschijnlijkheidsfunctie, die dezelfde functionele vorm heeft voor alle waarden van
volledig is verwijderd uit de waarschijnlijkheidsfunctie, die dezelfde functionele vorm heeft voor alle waarden van ![]() .
.
De Poisson-verdeling is geïmplementeerd in de WolframLanguage als PoissonDistribution.
Zoals verwacht wordt de Poisson-verdeling genormaliseerd zodat de som van de kansen gelijk is aan 1, aangezien
| |
(9 )
|
De verhouding van waarschijnlijkheden wordt gegeven door
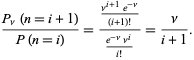 |
(10)
|
De Poisson-verdeling bereikt een maximum wanneer
| |
(11)
|
waarbij is de constante van Euler-Mascheroni en ![]() is een harmonisch getal dat leidt tot de transcendentale vergelijking
is een harmonisch getal dat leidt tot de transcendentale vergelijking
| |
(12)
|
wat niet exact kan worden opgelost voor ![]() .
.
De momentgenererende functie van de Poisson-verdeling wordt gegeven door
| |
|
|
(13)
|
| |
|
|
(14)
|
| |
|
|
(15)
|
| |
|
|
(16)
|
| |
|
|
(17)
|
| |
|
|
(18)
|
dus
| |
|
|
(19)
|
| |
|
|
(20)
|
(Papoulis 1984, p. 554).
De onbewerkte momenten kunnen ook direct worden berekend door sommatie, wat een onverwacht verband oplevert met de Bell-polynoom ![]() en Stirling-getallen van de tweede soort,
en Stirling-getallen van de tweede soort,
| |
(21)
|
bekend als de formule van Dobiński.Daarom
| |
|
|
(22)
|
| |
|
|
(23)
|
| |
|
|
(24)
|
De centrale momenten kunnen dan worden berekend als
| |
|
(25)
|
|
| |
|
|
(26)
|
| |
|
|
(27)
|
dus de gemiddelde, variantie, scheefheid en kurtosis-overmaat zijn
| |
|
|
(28)
|
| |
|
|
(29)
|
| |
|
|
(30)
|
| |
|
|
(31)
|
| |
|
|
(32)
|
De karakteristieke functie voor de Poissondistribution is
(Papoulis 1984, pp. 154 en 554), en de cumulant-genererende functie is
| |
(34)
|
dus
| |
(35)
|
De gemiddelde deviatie van de Poisson-verdeling wordt gegeven door
| |
(36)
|
De Poisson-verdeling kan ook worden uitgedrukt in termen van
| |
(37)
|
| |
(38)
|
De momentgenererende functie van een Poisson-verdeling in twee variabelen wordt gegeven door
| |
(39)
|
Als de onafhankelijke variabelen ![]() ,
, ![]() , …,
, …, ![]() hebben Poisson-verdelingen met parameters
hebben Poisson-verdelingen met parameters ![]() ,
, ![]() , …,
, …, ![]() , dan
, dan
| |
(40)
|
heeft een Poisson-verdeling met parameter
| |
(41)
|
Dit kan worden gezien aangezien de cumulant-genererende functie
| |
(42)
|
| |
(43)
|
Een generalisatie van de Poisson-verdeling is gebruikt door Saslaw (1989) om de waargenomen clustering van sterrenstelsels in het heelal. De vorm van deze distributie wordt gegeven door
| |
(44)
|
waarbij ![]() is het aantal sterrenstelsels in een volume
is het aantal sterrenstelsels in een volume ![]() ,
, ![]() ,
, ![]() is de gemiddelde dichtheid van sterrenstelsels, en
is de gemiddelde dichtheid van sterrenstelsels, en ![]() , met
, met ![]() is de verhouding tussen gravitatie-energie en kinetische energie van eigenaardige bewegingen, Letting
is de verhouding tussen gravitatie-energie en kinetische energie van eigenaardige bewegingen, Letting ![]() geeft
geeft
| |
(45)
|
wat inderdaad een Poisson-verdeling is met ![]() . Evenzo geeft
. Evenzo geeft ![]()
![]() .
.