Oppervlakte berekenen
Oppervlakte berekenen
Oppervlakte wordt gemeten in vierkanten (of vierkante eenheden).
Hoeveel vierkanten zijn er in deze rechthoek?

We kunnen de vierkanten tellen of we kunnen neem de lengte en breedte en gebruik vermenigvuldiging. De rechthoek hierboven heeft een oppervlakte van 15 vierkante eenheden.
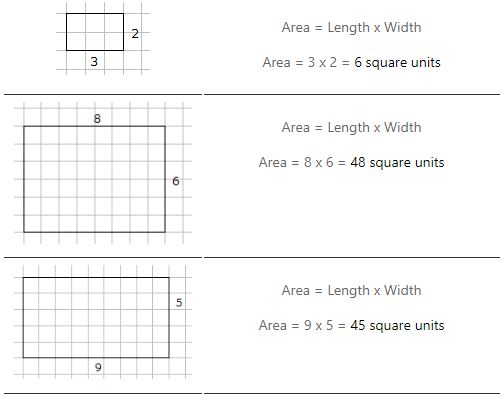
De oppervlakte van een rechthoek is = lengte x breedte
Voorbeelden van het berekenen van de oppervlakte van een rechthoek
Eenheden voor meetgebied
We meten oppervlakte met vierkanten. We gebruiken verschillende formaten vierkanten, afhankelijk van hoe groot of klein een gebied is.
| Voorbeeld | Lengte van zijde op vierkanten | Eenheid |
| Grootte van de spijker op je duim | Millimeter | mm2 |
| Formaat vel papier | Centimeter | cm2 |
| Grootte van een kamer | Meter | m2 |
| Grootte van een stad | Kilometer | km2 |
Vergeet de kleine 2 niet
We schrijven vierkante maten met een kleine 2 naast de eenheid.
We schrijven mm2, cm2, m2, km2, cm2
We kunnen zeggen “63 millimeter in het kwadraat” of “63 vierkante millimeter”
We zouden kleine vierkanten kunnen gebruiken om grote oppervlakken te meten. Het enige probleem hiermee is dat we uiteindelijk heel grote nummers. Een veld kan bijvoorbeeld worden gemeten op 5.000.000.000 vierkante millimeter, terwijl 5.000 vierkante meter een veel gemakkelijker formaat zou zijn om te zeggen, schrijven en visualiseren.
Je zult waarschijnlijk meer eenheden horen voor het meten van oppervlakte; vierkante inch, vierkante voet, vierkante meter, vierkante mijl, acres, hectare zijn allemaal eenheden die worden gebruikt voor het meten van oppervlakte.
Meer voorbeelden van het berekenen van oppervlakte
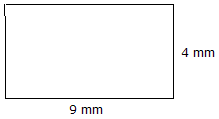 |
Gebied = lengte x breedte gebied = 9 mm x 4 mm = 36 mm2 |
 |
Gebied = Lengte x Breedte Gebied = 7 cm x 6 cm = 42 cm2 |
 |
Gebied = Lengte x Breedte Gebied = 8 mx 2 m = 16 m2 |
 |
Gebied = Lengte x Breedte Gebied = 7 km x 5 km = 35 km2 |
Oppervlakte van een vierkant
De lengte en breedte van een vierkant zijn hetzelfde, dus we hoeven de lengte alleen maar te vermenigvuldigen met de lengte.
| Area = Lengte x Lengte Area = 6 cm x 6 cm = 36 cm2 |
Oppervlakte van een cirkel
De oppervlakte van een cirkel = πr2
waarbij r de straal van de cirkel is en π de verhouding is tussen de omtrek van een cirkel en de diameter.
π (uitgesproken als taart en vaak geschreven als Pi) is een oneindig decimaal getal met een gemeenschappelijke benadering van 3.14159. Je kunt hier meer over Pi lezen
Voorbeeld van het berekenen van de oppervlakte van een cirkel
 |
Area = πr2 Area = 3.14159 x (4 cm) 2 Oppervlakte = 3,14159 x 16 cm2 Oppervlakte = 50,27 cm2 Antwoord afgerond op 2 decimalen |
Uitleg van de oppervlakte van een cirkelformule
Neem een cirkel en verdeel deze in even grote sectoren en herschik deze zoals hieronder weergegeven. Merk op hoe, naarmate de sectoren kleiner worden, de vorm meer als een rechthoek wordt. Opmerking: er is geen limiet aan hoe klein deze sectoren kunnen zijn en hoe nauw ze op een rechthoek kunnen lijken wanneer ze zijn gerangschikt.
Aangenomen dat we weten dat de omtrek van een cirkel gelijk is aan 2πr, kunnen we dimensies toevoegen aan de “rechthoek” zoals hieronder weergegeven. Met behulp van de oppervlakte van een rechthoekige gebiedsformule, oppervlakte = breedte x hoogte, kunnen we zien hoe onze cirkel, opnieuw geconfigureerd als een rechthoek, kan worden getoond als een oppervlakte die ongeveer overeenkomt met πr xr of πr2
Cirkel Sectoren opnieuw gerangschikt

Cirkelsectoren opnieuw gerangschikt – starten eruitzien als een rechthoek

Gebied van Samengestelde vormen
Er zijn veel gevallen waarin voor de berekening van een totale oppervlakte meer dan één oppervlakte moet worden berekend, gevolgd door een optelling, aftrekking of een andere combinatie van bewerkingen om de vereiste oppervlakte te vinden.
Opmerking: in de onderstaande voorbeelden worden de meeteenheden niet weergegeven en zijn de antwoorden en de waarde van π (Pi) afgerond op het dichtstbijzijnde honderdste.
Voorbeeld: eenvoudige samengestelde vormen
Het onderstaande voorbeeld van de gebiedsberekening is relatief eenvoudig. De vorm kan worden gezien als een driehoek gecombineerd met een rechthoek.
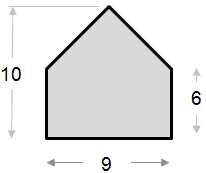 |
Oppervlakte van driehoekgedeelte: ½ x basis x hoogte ½ x 9 x 4 = 18 Oppervlakte van rechthoekig deel: Totale oppervlakte = 18 + 54 = 72 |
Het bovenstaande voorbeeld illustreert een algemene vereiste bij het werken met samengestelde vormen – afmetingen zoeken die niet worden weergegeven. Wanneer u uw kinderen bijles geeft, geef dan indien nodig hulp om deze “ontbrekende” dimensies te vinden. Hieronder staat nog een voorbeeld.
De afmetingen zoeken
 |
Wat zijn de afmetingen van het kleine rechthoekige deel? Breedte? 12 – 7 – 2 = 3 Hoogte? 8 – 6 = 2 |
Voorbeeld: het ene gebied van het andere aftrekken
In het onderstaande voorbeeld kan de vorm worden gezien als een rechthoek met een uitgesneden driehoek.
 |
Oppervlakte van rechthoekig deel: breedte x hoogte 5 x 6 = 30 Oppervlakte van driehoekig deel: Totale oppervlakte = 30 – 4.50 = 25.50 |
Voorbeeld: gedeeltelijke oppervlakken
Het onderstaande voorbeeld is vergelijkbaar met het bovenstaande voorbeeld, hoewel we, aangezien we een halve cirkel hebben, een breuk (een halve) moeten berekenen van het gebied van de cirkel. Let op in dit voorbeeld wordt de diameter weergegeven, en niet de straal.
 |
Oppervlakte van driehoekig deel: ½ x basis x hoogte ½ x 6 x 6 = 18 Oppervlakte van halfcirkelvormig deel: Totale oppervlakte = 18 – 3.53 = 14.47 |
Voorbeeld: beslissingen! Combineren? Aftrekken
Het is gebruikelijk dat er meer dan één manier is om de uiteindelijke oppervlakte te berekenen. In de onderstaande voorbeelden kan de vorm worden gezien als twee gecombineerde rechthoeken of als één grote rechthoek met een kleinere rechthoek “uitgesneden” uit de rechterbovenhoek.
Werkbladen berekenen voor oppervlakte
Afdrukken gebruik de onderstaande werkbladen en gebruik ze om te oefenen bij het lesgeven aan uw kinderen.
- Gebieden berekenen – rechthoeken en vierkanten
- Gebieden berekenen – rechthoeken
- Berekenen Gebieden – rechthoeken
- Samengestelde gebieden berekenen, bijv met rechthoekige vormen
- Berekenen van samengestelde gebieden, bijv. met rechthoeken, driehoeken en cirkels
- Gebieden berekenen, bijv. van driehoeken
- Oppervlakte van een cirkel
- Oppervlakte berekenen, bijv. van rechthoekige prismas
U vindt hier meer afdrukbare werkbladen voor geometrie.