Meting: formules voor oppervlakte ontdekken

formules voor oppervlakte

Studenten die het informele idee hebben dat oppervlakte de “hoeveelheid 2-D is spullen die zich in een regio bevinden, kunnen de meeste formules voor zichzelf verzinnen die ze vaak alleen maar uit het hoofd moeten leren. Elke formule die ze opnieuw uitvinden, helpt hun begrip (en geheugen) voor de andere formules die ze kennen te versterken. (Zie ook oppervlakte.)

Oppervlakte van rechthoeken

Door een vierkant als oppervlakte-eenheid te kiezen, krijgen we een intuïtief idee van de oppervlakte van rechthoeken. Als we besluiten dat de oppervlakte van dit vierkant 1 is, dan is een rechthoek die 7 keer zo lang is 7 × 1 als zijn oppervlakte.

Een rechthoek die tweemaal de hoogte is van zou tweemaal de oppervlakte hebben, dus de oppervlakte van is 2 × 7 oppervlakte-eenheden. We kunnen de twee rijen van zeven vierkanten tellen. Evenzo heeft 3 rijen van 7 vierkanten (of 7 kolommen van 3 vierkanten), voor een totaal van 7 × 3 vierkanten, dus de oppervlakte is 21 vierkante eenheden.

Het aantal vierkanten in een rij is de lengte van de rechthoek. Het aantal rijen is de hoogte van de rechthoek. Het gebied is dus lengte × hoogte.

Omdat een rechthoek schuin kan worden getekend, wordt met hoogte bedoeld de richting loodrecht op de basis en basis als, nou, welke kant je ook kiest.

Dat werkt voor het tellen van getallen. Het werkt zelfs voor breuken. 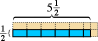De blauwe rechthoek die hier wordt weergegeven, meet de helft lengte-eenheid hoog bij vijf en een halve lengte-eenheid breed. Als we het overeenkomstige vierkant als onze oppervlakte-eenheid kiezen, zien we dat de blauwe rechthoek vijf halve eenheden van oppervlakte en een kwart eenheid van oppervlakte bevat, of een in totaal twee en driekwart oppervlakte-eenheden. (de roze delen tonen de voltooiing van elke vierkante oppervlakte-eenheid.)

Om alle getallen op te nemen, definiëren we het gebied van een rechthoek als basis × hoogte (waarbij “basis” en “hoogte” de lengtes van die zijden betekenen, gemeten in dezelfde eenheden).

Oppervlakte van parallellogrammen

Het idee krijgen

We kunnen een formule bedenken voor de oppervlakte van een parallellogram door te ontleden het parallellogram en de onderdelen opnieuw rangschikken om een rechthoek te maken. Omdat het parallellogram en de rechthoek uit dezelfde delen bestaan, hebben ze noodzakelijkerwijs hetzelfde oppervlak. (Zie de definitie van gebied voor meer informatie over waarom die gebieden hetzelfde zijn.)

We kunnen zien dat ze ook exact dezelfde basislengte (blauw) en exact dezelfde hoogte (groen). Omdat basis × hoogte de oppervlakte van de rechthoek geeft, kunnen we dezelfde metingen op het parallellogram gebruiken om de oppervlakte te berekenen: basis × hoogte. (Net als voorheen wordt hoogte loodrecht op de basis gemeten en is basis de zijde die u het eerst kiest. Zie parallellogram.)

De hierboven getoonde snede maakt het gemakkelijk om te zien dat de basislengte ongewijzigd. In feite kan de loodrechte snede overal langs de basis worden gemaakt.

Versteviging van de gaten

Intuïtie en bewijs

Deze dissectie geeft een intuïtief begrip van de gebiedsformule voor een parallellogram, een reden dat het zou moeten zijn zoals het is. Maar we hebben niet in twijfel getrokken of de dissectie echt werkt. Dat wil zeggen, wanneer we het parallellogram knippen en de onderdelen herschikken, verwachten we te krijgen en het resultaat ziet er zeker zo uit. Maar schijn kan bedrieglijk zijn. Wat verzekert ons dat wanneer we die driehoek verplaatsen, het resultaat een rechthoek is? Wat als het meer lijkt op (hoewel minder overdreven)? Als het resultaat niet altijd een perfecte rechthoek, we kunnen onze kennis van de oppervlakte-formule van de rechthoek niet gebruiken om een formule voor het parallellogram te ontwikkelen. Op de middelbare school zullen leerlingen kunnen bewijzen dat de twee delen van het parallellogram, wanneer ze correct in elkaar gezet zijn, een rechthoek vormen . In de klassen K-8 moeten leerlingen voor het grootste deel vertrouwen op het visuele experiment en een intuïtief gevoel krijgen. Meer informatie over waarom deze dissecties werken.

Wat als we de korte zijde als basis kiezen?

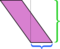
Het staat ons vrij om elke zijde als basis te kiezen; “hoogte” wordt gedefinieerd als te zijn gemeten loodrecht op de zijkant die we als basis kiezen. Als we de korte zijde (blauw) als basis nemen, is de bovenstaande dissectie niet zo overtuigend. Snijden langs die hoogte en het herschikken van de onderdelen laat een puinhoop achter:

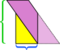
In dit specifieke voorbeeld, we kunnen de puinhoop redden door nog een snede te maken, 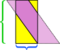maar wat als het parallellogram nog langer en magerder zou zijn?

Het blijkt dat elk parallellogram, hoe lang en mager ook, op deze manier kan worden ontleed, zodat de delen – misschien veel ervan – in een rechthoek kunnen worden herschikt. Maar er is meer werk voor nodig om te laten zien dat dit altijd kan. We hebben een ander idee nodig.

Een iets ander dissectie-idee maakt het leven in dit geval veel gemakkelijker. (U kunt zelf aantonen dat het ook werkt in het originele doosje.)

• Omsluit het parallellogram in een rechthoek.
• De twee delen van de rechthoek die niet binnen het parallellogram liggen, zijn congruente driehoeken.
• Schuif een van deze driehoeken naar de andere toe totdat ze samenkomen om een rechthoek te vormen. 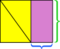Omdat de totale oppervlakte van de buitenste rechthoek niet is veranderd (het is dezelfde rechthoek als voorheen) en het gele gebied niet is veranderd (de stukken zijn net verplaatst), is het verschil tussen ze – de paarse gebieden – moeten hetzelfde zijn. Zoals eerder kunnen we ook zien dat de afmetingen van het rechthoekige paarse gebied de basis en hoogte zijn van het oorspronkelijke parallellogram.

Intuïtie en bewijs, herhaal : Nogmaals, de dissectie biedt het essentiële inzicht, maar het kost wat meer werk om ervoor te zorgen dat de twee gele driehoeken, die er zeker uitzien alsof ze in elkaar passen om een rechthoek te vormen, echt precies passen, en niet alleen bijna.

Waarom is het belangrijk om zo voorzichtig te zijn?

Wanneer we andere gebiedsformules bouwen (hieronder), zullen we onze manier willen gebruiken om het gebied van een parallellogram te vinden, en dus willen we om te kunnen vertrouwen op de regel die we hebben gevonden. We kunnen er zeker van zijn dat het herschikken van onderdelen het gebied niet verandert: dat is tenslotte hoe we het gebied definiëren. Maar we moeten er ook zeker van zijn dat de onderdelen in elkaar passen zoals we beweren dat ze doen, anders kunnen we niet vertrouwen op de metingen die we hebben gedaan. En we moeten er zeker van zijn dat de basis × hoogteregel niet afhangt van een gelukkige basiskeuze.

In de meeste curricula hebben studenten niet voldoende systematisch genoeg geometrische kennis geluid bewijst dat deze dissecties werken. Maar het intuïtieve begrip is voldoende om de formules uit te leggen en te rechtvaardigen, en een goede basis voor latere geometrische studie.

Oppervlakte van driehoek

Weten hoe we de oppervlakte van een parallellogram kunnen vinden, helpt ons vind de oppervlakte van een driehoek.

Ontleden van de driehoek

We kunnen de driehoek in twee delen ontleden – een van hen een driehoek en een van hen een trapezium – door hem parallel te snijden naar de basis. Als we de hoogte precies halveren met die plak, passen de twee delen in elkaar om een parallellogram te maken met dezelfde basis maar de helft van de hoogte.

Dus basis × halve hoogte geeft de oppervlakte van de driehoek. Een soortgelijke dissectie toont halve basis x hoogte. Elk van beide reduceert tot bh.

Verdubbeling van de driehoek en vervolgens halvering van het resulterende gebied

Een andere manier van denken: twee exemplaren van de driehoek maakt een parallellogram met dezelfde basis en dezelfde hoogte als de driehoek.

De oppervlakte van het parallellogram is basis × hoogte, maar dat is tweemaal de oppervlakte van de driehoek, dus de oppervlakte van de driehoek is van basis × hoogte, zoals we zagen met de dissectie-methode.

(Zoals altijd , kies een basis en meet de hoogte loodrecht op die basis, van de basis tot het tegenoverliggende hoekpunt.)

Oppervlakte van trapezium

Verdubbeling van de trapezium en halvering van het resulterende gebied

Zoals het geval was met de driehoek, kunnen twee kopieën van een trapezium in elkaar worden gepast om een parallellogram te maken.

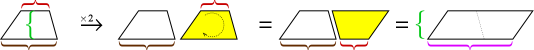
De hoogte van het parallellogram is gelijk aan de hoogte van het trapezium, maar de basis is de som van de twee bases van het trapezium. Het gebied van het parallellogram is dus hoogte × (basis1 + basis2). Maar dat gebied bestaat uit twee trapeziums, dus we moeten het doormidden snijden om het gebied van de trapezium te krijgen.

Het trapezium ontleden

We zouden het trapezium ook kunnen ontleden zoals we het hebben ontleed de driehoek, met een enkele plak die de hoogte doormidden snijdt. De twee delen passen in elkaar om een parallellogram te maken waarvan de basis de som is van de twee bases van de trapezium, maar waarvan de hoogte de helft is van de hoogte van de trapezium.

In het geval van de trapezium kunnen de bases niet worden naar believen gekozen. De twee parallelle zijden zijn de bases, en hoogte is, zoals altijd, de loodrechte afstand van de ene basis naar de andere.

De oppervlakte van dit parallellogram is de hoogte (halve hoogte van het trapezium) maal de basis (som van de bases van de trapezium), dus de oppervlakte is halve hoogte × (basis1 + basis2). Omdat het parallellogram is gemaakt van exact hetzelfde “materiaal” als het trapezium, is dat ook het gebied van het trapezium.

Hoe dan ook, het gebied van het trapezium is × hoogte × (base1 + base2).

Oppervlakte van andere speciale vierhoeken

Oppervlakte van ruit

De oppervlakte van een ruit kan worden gevonden door de stukken te knippen en opnieuw te rangschikken om een parallellogram te vormen. Dit kan op verschillende manieren worden gedaan:

1. Snijd over de kortere diagonaal (a) om twee congruente driehoeken te vormen. Verplaats de onderste helft van de driehoek naast de bovenste helft om een parallellogram te vormen. De kortere diagonaal (a) wordt de basis van het parallellogram en de helft van de langere diagonaal (b) wordt de hoogte van het parallellogram. De oppervlakte van de ruit is dus een * b of het product van de diagonalen, wat de standaardformule voor ruit is.
2. Een andere vergelijkbare manier is om de ruit in vier congruente driehoeken te snijden en ze opnieuw te rangschikken in een rechthoek met de kortere diagonaal als basis en de helft van de langere diagonaal als de hoogte.
3. Na het snijden de ruit in twee congruente driehoeken, kunnen we de oppervlakte van een van de driehoeken berekenen, die * basis (a) * hoogte ( b) = ab. Vermenigvuldig dan met twee, want er zijn er twee: 2 * ab = ab.

Oppervlakte van vlieger

Het gebied van een vlieger kan worden gevonden vergelijkbaar met het gebied van een ruit. Door over de langere diagonaal te snijden, worden twee congruente driehoeken verkregen. Als we ze herschikken, kunnen we een parallellogram vormen met de langere diagonaal (b) als basis en de helft van de kortere diagonaal (a) als de hoogte. Het gebied wordt dus b * a = ab. Een meer gecompliceerde benadering omvat een beetje algebra. Snijd de vlieger over de kortere diagonaal om twee driehoeken te vormen met de kortere diagonaal (a) als basis. Het gebied van de eerste driehoek is dus a * kronkelend, waarbij kronkelig de hoogte is. Het gebied van de tweede driehoek is a * (b – kronkelend), waarbij (b – kronkelend) het resterende deel is van de langere diagonaal. De totale oppervlakte wordt dus ( a * squiggly) + ( a * (b – squiggly)). Als we a buiten beschouwing laten, hebben we a (squiggly + b – squiggly) = ab.

Nou, wat weet je. In principe hoeft u alleen de formule voor de oppervlakte van een parallellogram te kennen en vervolgens de formule voor de andere af te leiden.