Het volume berekenen

Volume berekenen

Het volume wordt gemeten in kubussen (of kubieke eenheden).

Hoeveel kubussen zitten er in dit rechthoekige prisma (kubusvormig)?

We kunnen tellen de kubussen, hoewel het sneller is om de lengte, breedte en hoogte te nemen en vermenigvuldiging te gebruiken. Het rechthoekige prisma hierboven heeft een volume van 48 kubieke eenheden.

Het volume van een rechthoekig prisma is = lengte x breedte x hoogte

Voorbeelden van het berekenen van de oppervlakte van een rechthoek

We moeten twee vermenigvuldigingen doen om het volume te berekenen. We berekenen de oppervlakte van één vlak (of zijde) en vermenigvuldigen dat met de hoogte. De onderstaande voorbeelden laten zien hoe er drie manieren zijn om dit te doen.

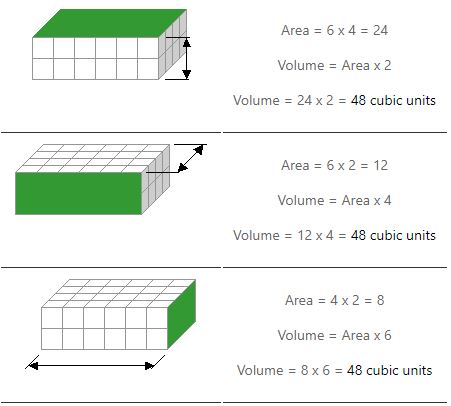
Merk op hoe we hetzelfde antwoord krijgen, ongeacht welke kant we gebruiken om een gebied te vinden.

Wanneer uw kind begint te werken met gebied en omtrek, zal hij of zij gewoonlijk met 2 dimensies werken – vierkanten, rechthoeken, driehoeken, enz. die op papier als plat worden weergegeven – er is geen diepte of 3e dimensie. Het werken met volume kent 3 dimensies. Zorg ervoor dat uw kind hiervan op de hoogte is en niet denkt dat de kubussen en andere 3D-vormen die op papier worden weergegeven, gewoon een andere “vorm op de pagina” zijn. Laat ze echte dozen zien en laat zien hoe deze op een tweedimensionaal vel papier kunnen worden getekend (of weergegeven). Met andere woorden, zorg ervoor dat er een verband is tussen wat op papier staat en wat het in de echte wereld vertegenwoordigt.

Zorg ervoor dat uw kind niet in de war raakt door het gebruik van het volume dat wordt gebruikt wanneer het over luidheid praat .

Eenheden voor het meten van volume

Er zijn zeer grote verschillen tussen de meeteenheden voor volume. Er zijn bijvoorbeeld 100 centimeter in 1 meter, maar er zijn 1.000.000 (ja, 1 miljoen ) kubieke centimeter in een kubieke meter.

Waarom het grote verschil? Omdat we in volume niet alleen lengte hebben; we hebben lengte, breedte en hoogte. Het voorbeeld van een suikerklontje hieronder laat dit zien.

Hoeveel suiker? 1 m3 of 1.000.000 cm3

Denk aan het vullen van een hele grote doos (hij zou 1 meter breed, 1 meter lang en een meter hoog zijn) met suikerklontjes (met elk zijde 1 centimeter).

	Stap 1: één rij langs de onderkant van het vak – dat zou 100 zijn suikerklontjes
	Stap 2: bedek de rest van de onderkant van de doos – dat zou in totaal 100 rijen opleveren met elk 100 suikerklontjes. 100 x 100 = 10.000 suikerklontjes onderin de grote doos.
	Stap 3: Herhaal dit 99 keer totdat er lagen van 10.000 blokjes 100 diep gestapeld. 10.000 x 100 = 1.000.000 suikerklontjes

Er zit 1.000.000 cm3 in 1 m3 – pas op dat je niet te veel suiker hebt!

Er zijn andere eenheden voor het meten van het volume; kubieke inch, kubieke voet, kubieke meter zijn allemaal eenheden die worden gebruikt voor het meten van het volume. Milliliter, liter, gallon worden ook vooral gebruikt bij het afmeten van vloeistoffen.

Vergeet de kleine 3 niet

We schrijven kubieke maten met een kleine 3 naast de eenheid.
We schrijven mm3, cm3, m3, km3, cm3
We kunnen zeggen “85 centimeter in blokjes” of “85 kubieke centimeter”

Voorbeelden van het berekenen van het volume van rechthoekige prismas

	Volume = lengte x breedte x hoogte Volume = 12 cm x 8 cm x 6 cm = 576 cm3
	Volume = lengte x breedte x hoogte Volume = 20 mx 2 mx 2 m = 80 m3
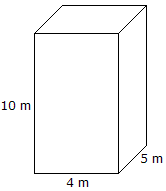	Volume = lengte x breedte x Hoogte Volume = 10 mx 4 mx 5 m = 200 m3

Volume van een cilinder

Het volume van een cilinder berekenen Der omvat het vermenigvuldigen van het oppervlak van de basis met de hoogte van de cilinder. De basis van een cilinder is cirkelvormig en de formule voor de oppervlakte van een cirkel is: oppervlakte van een cirkel = πr2. Er is hier meer over de oppervlakte van een cirkel.

Volume = Oppervlakte van basis x Hoogte Volume = πr2 xh Volume = πr2 h

Opmerking: in de onderstaande voorbeelden we zullen 3.14 gebruiken als een geschatte waarde voor π (Pi).

Voorbeeld van het berekenen van het volume van een cilinder

Afmetingen zijn in cm.

Volume = πr2 h Volume = 3.14 x 3 x 3 x 8 Volume = 226,08 cm3

Volume van een kegel

Het volume van een kegel is gelijk aan een derde van het volume van een cilinder met bijpassende hoogte en oppervlakte van de basis. Dit geeft de formule voor het volume van een kegel zoals hieronder weergegeven.

Volume = 1/3 πr2h

Voorbeeld van het berekenen van het volume van een kegel

Afmetingen zijn in cm.

Inhoud = 1/3 πr2 h Inhoud = 1/3 x 3,14 x 2 x 2 x 7 Inhoud = 29,31 cm3

Volume van een bol

De formule voor het volume van een bol wordt hieronder weergegeven.

Volume = 4/3 πr3

Voorbeeld van het berekenen van het volume van een bol

Afmetingen zijn in cm.

Volume = 4/3 πr3 Volume = 4/3 x 3,14 x 4 x 4 x 4 Volume = 267,95 cm3

Werkbladen voor afdrukbaar volume

Gebruik het onderstaande werkblad om te oefenen met het berekenen van volumes.

• Het vinden van volume in kubieke eenheden – rechthoekige prismas en composieten
• Volumes van rechthoekige prismas
• Volumes van rechthoekige prismas
• Volumes van Real-world-objecten, bijv. van dozen met granen
• Volumes berekenen, bijv. van driehoekige prismas en cilinders

Je krijgt hier andere geometrie-werkbladen over omtrek, oppervlakte en meer.