Exponentiële verdeling
door Marco Taboga, PhD
De exponentiële verdeling is een continue kansverdeling die wordt gebruikt om modelleer de tijd die we moeten wachten voordat een bepaalde gebeurtenis plaatsvindt. Het is de continue tegenhanger van de geometrische verdeling, die in plaats daarvan discreet is.
Soms wordt het ook wel negatieve exponentiële verdeling genoemd.
Inleiding
Hoeveel tijd zal er verstrijken voordat zich een aardbeving voordoet in een bepaalde regio? Hoe lang moeten we wachten tot een klant onze winkel binnenkomt? Hoe lang duurt het voordat een callcenter het volgende telefoontje ontvangt? Hoe lang zal een machine werken zonder kapot te gaan?
Vragen zoals deze worden vaak in probabilistische termen beantwoord door de exponentiële verdeling te gebruiken.
Al deze vragen hebben betrekking op de tijd die we nodig hebben om te wachten voordat een bepaalde gebeurtenis plaatsvindt. Als deze wachttijd onbekend is, is het vaak gepast om deze te beschouwen als een willekeurige variabele met een exponentiële verdeling.
Globaal gesproken hebben we de tijd 
nodig wachten voordat een gebeurtenis plaatsvindt, heeft een exponentiële verdeling als de kans dat de gebeurtenis zich voordoet gedurende een bepaald tijdsinterval evenredig is met de lengte van dat tijdsinterval.
Meer precies, heeft een exponentiële verdeling als de voorwaardelijke kans ongeveer evenredig is met de lengte van het tijdsinterval tussen de tijden en , voor elk moment .
In veel praktijksituaties is deze eigenschap zeer realistisch. Dit is de reden waarom de exponentiële verdeling zo veel wordt gebruikt om wachttijden te modelleren.
De exponentiële verdeling is strikt gerelateerd aan de Poisson-verdeling. Als 1) een gebeurtenis meer dan eens kan voorkomen en 2) de tijd die is verstreken tussen twee opeenvolgende gebeurtenissen exponentieel verdeeld en onafhankelijk is van eerdere gebeurtenissen, dan heeft het aantal gebeurtenissen van de gebeurtenis binnen een gegeven tijdseenheid een Poisson-verdeling. We nodigen de lezer uit om de lezing over de Poisson-verdeling te zien voor een meer gedetailleerde uitleg en een intuïtieve grafische weergave van dit feit.
Definitie
De exponentiële verdeling wordt als volgt gekarakteriseerd. / p>
Definitie Laat een continue willekeurige variabele zijn. Laat zijn ondersteuning de reeks positieve reële getallen zijn: Laat . We zeggen dat een exponentiële verdeling heeft met parameter als en slechts als de kansdichtheidsfunctie De parameter wordt de tariefparameter genoemd.
Een willekeurige variabele met een exponentiële verdeling wordt ook wel een exponentiële willekeurige variabele genoemd.
Het volgende is een bewijs dat is een legitieme kansdichtheidsfunctie.
Niet-negativiteit is duidelijk. We moeten bewijzen dat de integraal van en gelijk is aan . Dit wordt als volgt bewezen:
Om de exponentiële verdeling beter te begrijpen, kunt u de dichtheidsplots ervan bekijken.
De tariefparameter en zijn interpretatie
We hebben vermeld dat de kans dat de gebeurtenis plaatsvindt tussen twee datums en is evenredig met (afhankelijk van de informatie dat het niet is voorgekomen vóór ). De tariefparameter is de evenredigheidsconstante: waarbij een oneindig klein aantal is van hogere volgorde dan (dwz een functie van die sneller naar nul gaat dan doet).
De bovenstaande evenredigheidsvoorwaarde is ook voldoende om de exponentiële verdeling volledig te karakteriseren.
Propositie De evenredigheidsvoorwaarde is alleen tevreden als een exponentiële verdeling heeft.
De voorwaardelijke kans kan worden geschreven als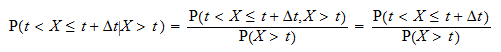 
Duid met de distributiefunctie van aan, dat wil zeggen en door zijn overlevingsfunctie: Vervolgens Beide zijden delen door , we krijgen waar een hoeveelheid is die neigt naar wanneer neigt naar . Door grenzen aan beide kanten te nemen, verkrijgen we of, volgens de definitie van afgeleide: Deze differentiaalvergelijking is eenvoudig op te lossen door de ketting te gebruiken rule: Als we de integraal nemen van naar van beide kanten, krijgen we en of Maar (omdat geen negatieve waarden kan aannemen) impliceert Exponentiërend aan beide zijden, verkrijgen we Daarom of Maar de dichtheidsfunctie is de eerste afgeleide van de verdelingsfunctie: en de meest rechtse term is de dichtheid van een exponentiële willekeurige variabele. Daarom wordt alleen aan de evenredigheidsvoorwaarde voldaan als een exponentiële willekeurige variabele is
Verwachte waarde
De verwachte waarde van een exponentiële willekeurige variabele is
Het kan als volgt worden afgeleid: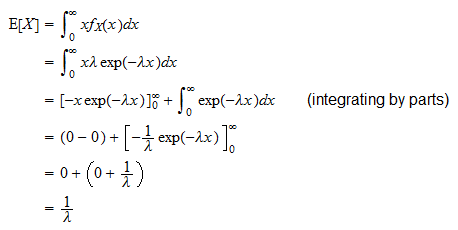 
Variantie
De variantie van een exponentiële willekeurige variabele is
Het kan worden afgeleid dankzij de gebruikelijke variantieformule (): 
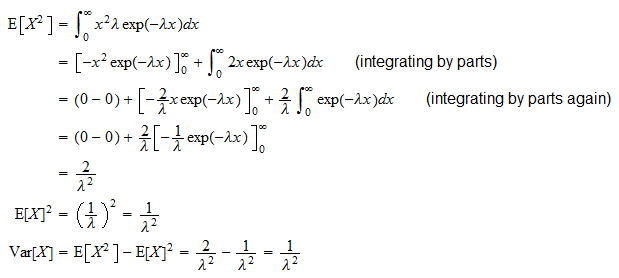
Momentgenererende functie
De momentgenererende functie van een exponentiële willekeurige variabele is gedefinieerd voor elke :
De definitie van momentgenererende functie geeft Van natuurlijk convergeren de bovenstaande integralen alleen als , d.w.z. alleen als . Daarom bestaat de momentgenererende functie van een exponentiële willekeurige variabele voor alle .
Karakteristieke functie
De karakteristieke functie van een exponentiële willekeurige variabele is
Door gebruik te maken van de definitie van karakteristieke functie en het feit dat we kunnen schrijven We berekenen nu afzonderlijk de twee integralen . De eerste integraal is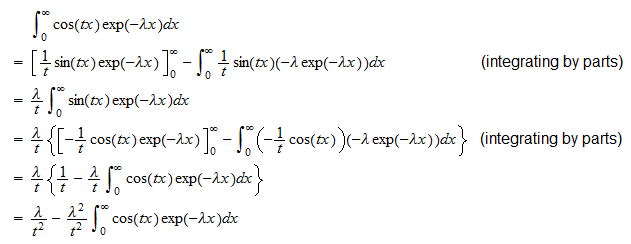 
Daarom die kan worden herschikt om of De tweede integraal is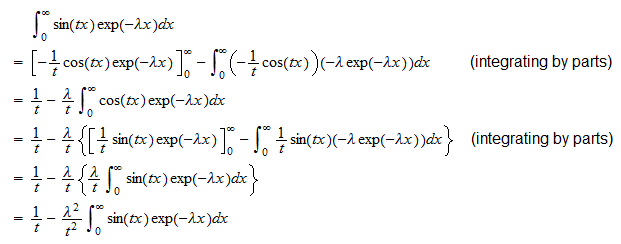 
Daarom kan worden herschikt om of Door stukjes samen te voegen, krijgen we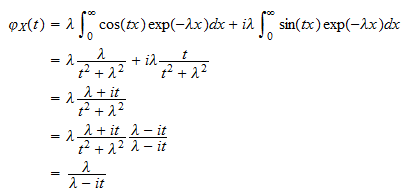 
Distributiefunctie
De distributiefunctie van een exponentiële willekeurige variabele is
Als , dan omdat kan geen negatieve waarden aannemen. Als , dan
Meer details
In de volgende paragrafen vindt u meer details over de exponentiële verdeling.
Geheugenloze eigenschap
Een van de belangrijkste eigenschappen van de exponentiële verdeling is de geheugenloze eigenschap: voor elke .
Dit wordt als volgt bewezen: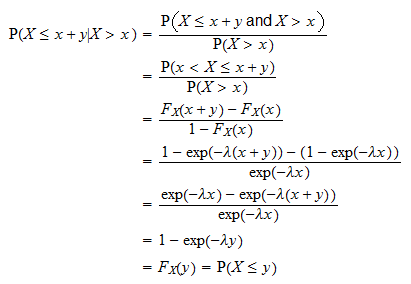 
is de tijd die we moeten wachten op een bepaalde gebeurtenis treedt op. De bovenstaande eigenschap zegt dat de kans dat de gebeurtenis plaatsvindt gedurende een tijdsinterval van onafhankelijk is van hoeveel tijd er al is verstreken () zonder dat de gebeurtenis plaatsvindt.
De som van exponentiële willekeurige variabelen is een willekeurige Gamma-variabele
Stel dat , , …, zijn onderling onafhankelijke willekeurige variabelen met exponentiële distributie met parameter .
Definieer
Vervolgens is de som een willekeurige Gamma-variabele met parameters en .
Dit is bewezen met moment genererende functies (onthoud dat de momentgenererende functie van een som van onderling onafhankelijke willekeurige variabelen slechts het product is van hun momentgenererende functies): Dit laatste is de momentgenererende functie van een Gamma distributie met parameters en . Dus heeft een Gamma-verdeling, omdat twee willekeurige variabelen dezelfde verdeling hebben als ze dezelfde momentgenererende functie hebben.
Van de willekeurige variabele wordt soms ook gezegd dat deze een Erlang-distributie heeft. De Erlang-verdeling is slechts een speciaal geval van de Gamma-verdeling: een willekeurige Gamma-variabele is ook een willekeurige Erlang-variabele als deze kan worden geschreven als een som van exponentiële willekeurige variabelen.
Dichtheidsgrafiek
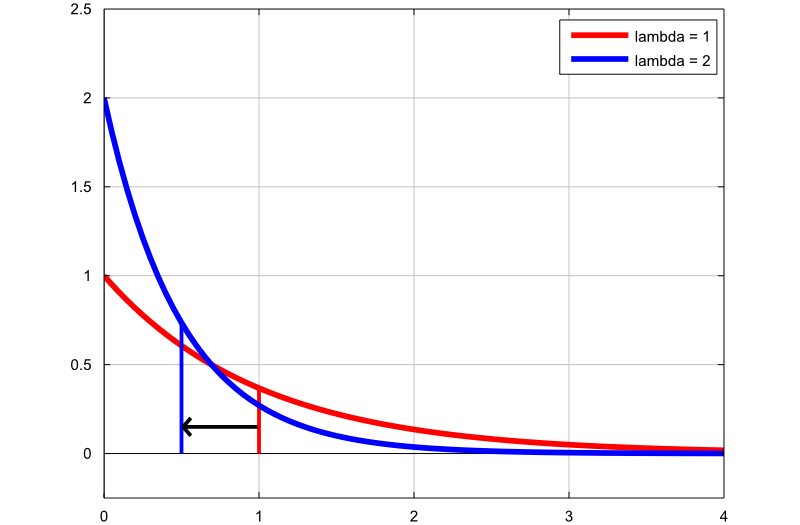
De volgende grafiek laat zien hoe de dichtheid van de exponentiële verdeling verandert door de snelheidsparameter te veranderen:
-
de eerste grafiek (rode lijn) is de kansdichtheidsfunctie van een exponentiële willekeurige variabele met tariefparameter
; -
de tweede grafiek (blauwe lijn) is de kansdichtheidsfunctie van een exponentiële willekeurige variabele met tariefparameter
.
De dunne verticale lijnen geven de gemiddelden van de twee verdelingen aan. Merk op dat door het verhogen van de rate-parameter, we het gemiddelde van de distributie verlagen van naar .
Opgeloste oefeningen
Hieronder vind je enkele oefeningen met uitgelegd oplossingen.
Oefening 1
Laat een exponentiële willekeurige variabele zijn met parameter . Bereken de volgende kans:
Allereerst kunnen we de kans schrijven als gebruikmakend van het feit dat de kans dat een continue willekeurige variabele een specifieke waarde aanneemt gelijk is aan nul (zie Continue willekeurige variabelen en nulwaarschijnlijkheidsgebeurtenissen). Nu kan de kans worden geschreven in termen van de verdelingsfunctie van als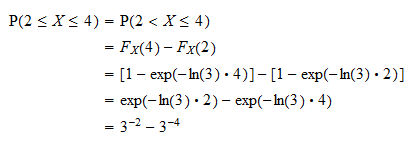 
Oefening 2
Stel dat de willekeurige variabele een exponentiële verdeling heeft met parameter . Bereken de volgende kans:
Deze kans kan eenvoudig worden berekend met behulp van de verdelingsfunctie van :
Oefening 3
Wat is de kans dat een willekeurige variabele is kleiner dan de verwachte waarde, als een exponentiële verdeling heeft met parameter ?
De verwachte waarde van een exponentiële willekeurige variabele met parameter is De bovenstaande waarschijnlijkheid kan worden berekend door de verdelingsfunctie van :
Hoe te citeren
Gelieve te citeren als: