College-algebra (Nederlands)
Door naar de grafiek van een rationele functie te kijken, kunnen we het lokale gedrag ervan onderzoeken en gemakkelijk zien of er asymptoten zijn. We kunnen mogelijk zelfs hun locatie benaderen. Zelfs zonder de grafiek kunnen we echter nog steeds bepalen of een bepaalde rationale functie asymptoten heeft, en hun locatie berekenen.
Verticale asymptoten
De verticale asymptoten van een rationale functie kunnen gevonden door de factoren van de noemer te onderzoeken die niet gemeenschappelijk zijn voor de factoren in de teller. Verticale asymptoten komen voor op de nullen van dergelijke factoren.
Hoe: Gegeven een rationele functie, identificeer eventuele verticale asymptoten van de grafiek.
- Factor de teller en noemer.
- Let op eventuele beperkingen in het domein van de functie.
- Verklein de uitdrukking door gemeenschappelijke factoren in de teller en de noemer op te heffen.
- Let op eventuele waarden die ervoor zorgen dat de noemer nul is in deze vereenvoudigde versie. Dit zijn waar de verticale asymptoten voorkomen.
- Let op eventuele beperkingen in het domein waar asymptoten niet voorkomen. Dit zijn verwijderbare onderbrekingen.
Verwijderbare onderbrekingen
Af en toe bevat een grafiek een gat: een enkel punt waar de grafiek niet is gedefinieerd, aangegeven door een open cirkel. We noemen zon gat een verwijderbare discontinuïteit.
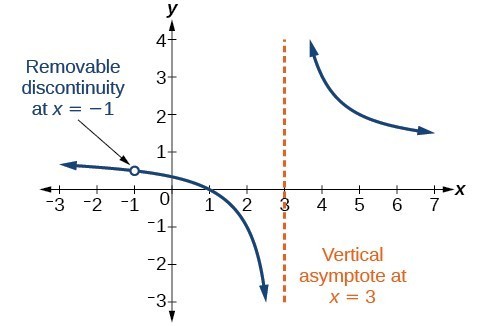
Figuur 10
Een algemene opmerking: verwijderbare onderbrekingen van rationele functies
Er treedt een verwijderbare discontinuïteit op in de grafiek van een rationale functie bij x = a als a een nul is voor een factor in de noemer die gemeenschappelijk is met een factor in de teller. We factoreren de teller en de noemer en zoeken naar gemeenschappelijke factoren. Als we er een vinden, stellen we de gemeenschappelijke factor gelijk aan 0 en lossen we op. Dit is de locatie van de verwijderbare discontinuïteit. Dit is waar als de multipliciteit van deze factor groter is dan of gelijk is aan die in de noemer. Als de veelheid van deze factor groter is in de noemer, dan is er nog steeds een asymptoot bij die waarde.
Horizontale asymptoten
Terwijl verticale asymptoten het gedrag van een grafiek als de uitvoer erg groot of erg klein wordt, horizontale asymptoten helpen bij het beschrijven van het gedrag van een grafiek als de invoer erg groot of erg klein wordt. Bedenk dat het eindgedrag van een polynoom dat van de leidende term zal weerspiegelen. Evenzo zal het eindgedrag van een rationele functie dat van de verhouding tussen de leidende termen van de teller- en noemerfuncties weerspiegelen.
Er zijn drie verschillende uitkomsten bij het controleren op horizontale asymptoten:
Geval 1: Als de graad van de noemer > graad van de teller, is er een horizontale asymptoot op y = 0.

Geval 2: Als de graad van de noemer < graad van de teller één is, krijgen we een schuine asymptoot.

Merk op dat, hoewel de grafiek van een rationale functie nooit een verticale asymptoot zal kruisen, de grafiek kan al dan niet een horizontale of schuine asymptoot. Ook, hoewel de grafiek van een rationale functie veel verticale asymptoten kan hebben, zal de grafiek maximaal één horizontale (of schuine) asymptoot hebben.
Opgemerkt moet worden dat, als de graad van de teller groter is dan de graad van de noemer met meer dan één, zal het eindgedrag van de grafiek het gedrag van de verminderde eindgedragsfractie nabootsen. Als we bijvoorbeeld de functie
met eindgedrag
het eindgedrag van de grafiek zou lijken op dat van een even polynoom met een positieve leidende coëfficiënt.
Een algemene opmerking: horizontale asymptoten van Rationale functies
De horizontale asymptoot van een rationale functie kan worden bepaald door te kijken naar de graden van de teller en de noemer.
- De graad van de teller is kleiner dan de graad van de noemer: horizontale asymptoot op y = 0.
- Mate van teller is één groter dan graad van noemer: geen horizontale asymptoot; schuine asymptoot.
- Mate van teller is gelijk aan graad van noemer: horizontale asymptoot bij verhouding van leidende coëfficiënten.
Een algemene opmerking: onderscheppingen van rationale functies
Een rationele functie heeft een y-snijpunt als de invoer nul is, als de functie is gedefinieerd op nul. Een rationele functie zal geen y-snijpunt hebben als de functie niet op nul is gedefinieerd.
Evenzo zal een rationale functie x-onderscheppingen hebben bij de ingangen die ervoor zorgen dat de uitvoer nul is. Omdat een breuk alleen gelijk is aan nul als de teller nul is, kunnen x-intercepts alleen voorkomen als de teller van de rationale functie gelijk is aan nul.
Probeer het 7
Gegeven de reciproque gekwadrateerde functie die 3 eenheden naar rechts en 4 eenheden omlaag is verschoven, schrijf dit dan als een rationele functie. Zoek vervolgens de x– en y-intercepts en de horizontale en verticale asymptoten.
Oplossing