College-algebra
Leerresultaten
- Identificeer het hoekpunt, de symmetrieas, het y-snijpunt en de minimale of maximale waarde van een parabool van het is een grafiek.
- Identificeer een kwadratische functie geschreven in algemene en hoekpuntvorm.
- Gegeven een kwadratische functie in algemene vorm, zoek het hoekpunt.
- Definieer het domein en bereik van een kwadratische functie door het hoekpunt te identificeren als een maximum of minimum.
De grafiek van een kwadratische functie is een U-vormige curve die een parabool wordt genoemd. Een belangrijk kenmerk van de grafiek is dat deze een extreem punt heeft, de vertex. Als de parabool opengaat, vertegenwoordigt het hoekpunt het laagste punt op de grafiek, of de minimumwaarde van de kwadratische functie. Als de parabool naar beneden opent, vertegenwoordigt het hoekpunt het hoogste punt van de grafiek, of de maximale waarde. In beide gevallen is het hoekpunt een keerpunt in de grafiek. De grafiek is ook symmetrisch met een verticale lijn door het hoekpunt, de zogenaamde symmetrieas.
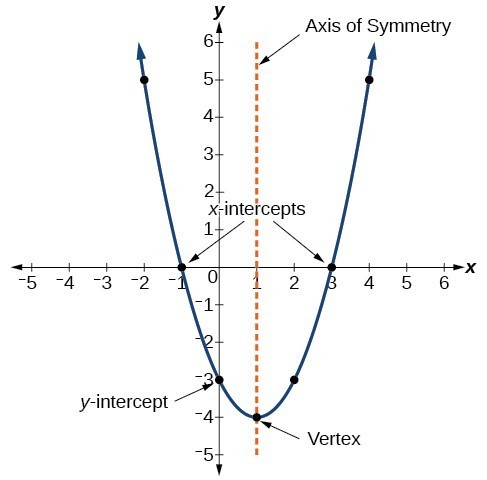
Vergelijkingen van kwadratische functies
De algemene vorm van een kwadratische functie presenteert de functie in de vorm
f \ left (x \ right) = a {x} ^ {2} + bx + c
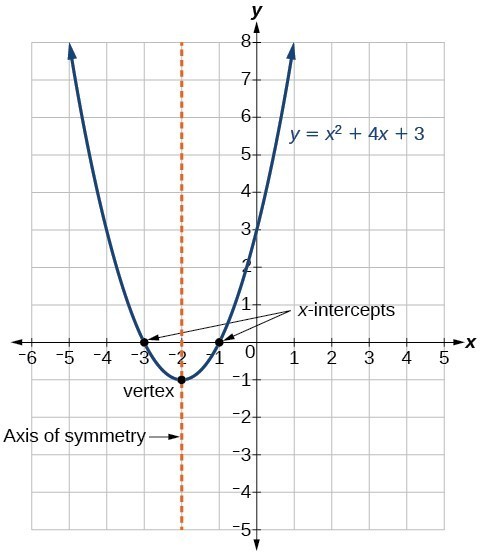
De standaardvorm van een kwadratische functie presenteert de functie in de vorm
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Gegeven een kwadratische functie in het algemeen zoek het hoekpunt van de parabool.
Een reden waarom we het hoekpunt van de parabool willen identificeren, is dat dit punt ons zal informeren waar de maximale of minimale waarde van de uitvoer voorkomt, k, en waar het komt voor, h. Als we de algemene vorm van een kwadratische functie krijgen:
f (x) = ax ^ 2 + bx + c
We kunnen definiëren het hoekpunt, (h, k), door het volgende te doen:
Het domein en bereik van een kwadratische functie zoeken
Elk getal kan de invoerwaarde van een kwadratische functie zijn. Daarom is het domein van elke kwadratische functie allemaal reële getallen. Omdat parabolen een maximum of een minimum hebben aan de top, is het bereik beperkt. Aangezien de top van een parabool ofwel een maximum of een minimum zal zijn, zal het bereik bestaan uit alle y-waarden groter dan of gelijk aan de y-coördinaat van de top of kleiner dan of gelijk aan de y-coördinaat op het keerpunt. , afhankelijk van of de parabool omhoog of omlaag opent.
Draag bij!
Verbeter deze paginaMeer informatie