Messung: Formeln für Fläche ermitteln

Flächenformeln

Schüler, die informell davon ausgehen, dass Fläche die „Menge von 2-D“ ist In einer Region enthaltenes Zeug kann die meisten Formeln, die sie oft nur auswendig lernen sollen, für sich selbst erfinden. Jede Formel, die sie neu erfinden, stärkt ihr Verständnis (und Gedächtnis) für die anderen Formeln, die sie kennen. (Siehe auch Oberfläche.)

Fläche von Rechtecken

Durch Auswahl eines Quadrats als Flächeneinheit erhalten wir eine intuitive Vorstellung von der Fläche von Rechtecken. Wenn wir entscheiden, dass die Fläche dieses Quadrats 1 ist, hat ein Rechteck , das siebenmal so lang ist, 7 × 1

Ein Rechteck, das doppelt so hoch wie ist, hätte die doppelte Fläche, also die Fläche von ist 2 × 7 Flächeneinheiten. Wir können die zwei Reihen von sieben Quadraten zählen. In ähnlicher Weise hat 3 Zeilen mit 7 Quadraten (oder 7 Spalten mit 3 Quadraten) für insgesamt 7 × 3 Quadrate, sodass seine Fläche 21 Quadrateinheiten beträgt.

Die Anzahl der Quadrate in einer Reihe entspricht der Länge des Rechtecks. Die Anzahl der Zeilen entspricht der Höhe des Rechtecks. Die Fläche ist also Länge × Höhe.

Da ein Rechteck schräg gezeichnet werden kann, bedeutet „Höhe“ „die Richtung senkrecht zur Basis“ und „Basis“: Nun, egal für welche Seite Sie sich entscheiden.

Das funktioniert zum Zählen von Zahlen. Es funktioniert sogar für Brüche. 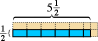Das hier gezeigte blaue Rechteck misst die Hälfte Längeneinheit hoch um fünfeinhalb Längeneinheiten breit. Wenn wir das entsprechende Quadrat als Flächeneinheit wählen, sehen wir, dass das blaue Rechteck fünf halbe Flächeneinheiten und eine Vierteleinheit Fläche enthält, oder a Insgesamt zwei- und dreiviertel Flächeneinheiten. (Die rosa Teile zeigen die Vervollständigung jeder quadratischen Flächeneinheit.)

Um alle Zahlen einzuschließen, definieren wir die Fläche eines Rechtecks als Basis × Höhe (wobei „Basis“ und „Höhe“ die Länge dieser Seiten bedeuten, gemessen in denselben Einheiten).

Bereich der Parallelogramme

Auf die Idee kommen

Wir können eine Formel für die Fläche eines Parallelogramms durch Präparieren herausfinden Parallelogramm erstellen und die Teile neu anordnen, um ein Rechteck zu bilden. Da das Parallelogramm und das Rechteck aus denselben Teilen bestehen, haben sie notwendigerweise dieselbe Fläche. (Weitere Informationen dazu, warum diese Bereiche identisch sind, finden Sie in der Definition des Bereichs.)

Wir können sehen, dass sie auch vorhanden sind genau die gleiche Grundlänge (blau) und genau die gleiche Höhe (grün). Da Basis × Höhe die Fläche des Rechtecks angibt, können wir die gleichen Maße für das Parallelogramm verwenden, um seine Fläche zu berechnen: Basis × Höhe. (Wie zuvor wird „Höhe“ senkrecht zur Basis gemessen, und „Basis“ ist die Seite, die Sie zuerst ausgewählt haben. Siehe Parallelogramm.)

Der oben gezeigte Schnitt macht es leicht zu erkennen, dass die Basislänge ist unverändert. Tatsächlich kann der senkrechte Schnitt überall entlang der Basis vorgenommen werden.

Stützen der Löcher

Intuition und Beweis

Diese Dissektion vermittelt ein intuitives Verständnis der Flächenformel für ein Parallelogramm, ein Grund, warum es so sein sollte, wie es ist. Aber wir haben nicht in Frage gestellt, ob die Dissektion wirklich „funktioniert“. Das heißt, wenn wir das Parallelogramm schneiden und seine Teile neu anordnen, erwarten wir und das Ergebnis sieht auf jeden Fall so aus Erscheinungen können täuschen. Was versichert uns, dass das Ergebnis beim Verschieben dieses Dreiecks ein Rechteck ist? Was ist, wenn es eher ist (wenn auch weniger übertrieben)? Wenn das Ergebnis nicht ist Immer ein perfektes Rechteck, wir können unser Wissen über die Flächenformel des Rechtecks nicht verwenden, um eine Formel für das Parallelogramm zu entwickeln. In der High School können die Schüler nachweisen, dass die beiden Teile des Parallelogramms, wenn sie richtig zusammengesetzt werden, ein Rechteck bilden In den Klassen K-8 müssen sich die Schüler größtenteils auf das visuelle Experiment verlassen und ein intuitives Gefühl bekommen. Erfahren Sie mehr darüber, warum diese Präparationen funktionieren.

Was ist, wenn wir die kurze Seite als Basis auswählen?

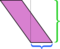
Wir können jede Seite als Basis auswählen; „height“ ist definiert als gemessen senkrecht zur Seite wählen wir als Basis. Wenn wir die kurze Seite (blau) als Basis nehmen, ist die oben gezeigte Präparation nicht so überzeugend. Das Schneiden entlang dieser Höhe und das Neuanordnen der Teile hinterlässt ein Durcheinander:

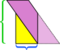
In diesem speziellen Beispiel Wir können das Chaos retten, indem wir einen weiteren Schnitt machen, 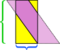, aber was wäre, wenn das Parallelogramm noch länger und dünner wäre?

Es stellt sich heraus, dass jedes noch so lange und dünne Parallelogramm auf diese Weise zerlegt werden kann, sodass die Teile – vielleicht viele von ihnen – zu einem Rechteck neu angeordnet werden können. Es erfordert jedoch mehr Arbeit, um zu zeigen, dass dies immer möglich ist. Wir brauchen eine andere Idee.

Eine etwas andere Präparationsidee erleichtert in diesem Fall das Leben erheblich. (Sie können selbst zeigen, dass dies auch im Originalfall funktioniert.)

• Schließen Sie das Parallelogramm in ein Rechteck ein.
• Die beiden Teile des Rechtecks, die sich nicht innerhalb des Parallelogramms befinden, sind kongruente Dreiecke.
• Schieben Sie eines dieser Dreiecke in Richtung des anderen, bis sie sich treffen, um ein Rechteck zu bilden. 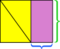Da sich die Gesamtfläche des äußeren Rechtecks nicht geändert hat (es ist das gleiche Rechteck wie zuvor) und sich die gelbe Fläche nicht geändert hat (die Teile haben sich gerade bewegt), ist der Unterschied zwischen sie – die lila Bereiche – müssen gleich sein. Nach wie vor können wir auch sehen, dass die Abmessungen des rechteckigen violetten Bereichs die Basis und Höhe des ursprünglichen Parallelogramms sind.

Intuition und Beweis, Wiederholung : Auch hier liefert die Präparation die wesentlichen Erkenntnisse, aber es erfordert etwas mehr Arbeit, um sicherzustellen, dass die beiden gelben Dreiecke, die mit Sicherheit so aussehen, als würden sie zu einem Rechteck zusammenpassen, wirklich genau passen und nicht nur fast.

Warum ist es wichtig, so vorsichtig zu sein?

Wenn wir andere Flächenformeln erstellen (siehe unten), möchten wir unsere Methode zum Ermitteln der Fläche eines Parallelogramms verwenden, und so wollen wir sich auf die Regel verlassen zu können, die wir gefunden haben. Wir können sicher sein, dass das Neuanordnen von Teilen den Bereich nicht verändert. So definieren wir schließlich den Bereich. Wir müssen aber auch sicher sein, dass die Teile so zusammenpassen, wie wir es behaupten, oder wir können uns nicht auf die Messungen verlassen, die wir durchgeführt haben. Und wir müssen sicher sein, dass die Basis × Höhenregel nicht von einer glücklichen Wahl der Basis abhängt.

In den meisten Lehrplänen verfügen die Schüler vor der 8. Klasse nicht über eine systematisch genug geometrische Basis Schallnachweise, dass diese Präparationen funktionieren. Das intuitive Verständnis reicht jedoch aus, um die Formeln zu erklären und zu rechtfertigen, und eine gute Grundlage für spätere geometrische Untersuchungen.

Dreiecksfläche

Es hilft uns, zu wissen, wie man die Fläche eines Parallelogramms findet Finden Sie die Fläche eines Dreiecks.

Zerlegen des Dreiecks

Wir können das Dreieck in zwei Teile zerlegen – einen davon als Dreieck und einen als Trapez – indem wir es parallel schneiden zur Basis. Wenn wir die Höhe mit dieser Scheibe genau halbieren, passen die beiden Teile zusammen, um ein Parallelogramm mit derselben Basis, aber der halben Höhe zu erstellen.

Basis × halbe Höhe gibt also die Fläche des Dreiecks an. Eine ähnliche Präparation zeigt die halbe Basis × Höhe. Beide reduzieren sich auf bh.

Verdoppeln des Dreiecks und anschließende Halbierung des resultierenden Bereichs

Eine andere Denkweise: zwei Kopien von Das Dreieck erstellt ein Parallelogramm mit derselben Basis und Höhe wie das Dreieck.

Die Fläche des Parallelogramms ist Basis × Höhe. Dies ist jedoch die doppelte Fläche des Dreiecks, sodass die Fläche des Dreiecks der Basis × Höhe ist, wie wir bei der Dissektionsmethode gesehen haben.

(Wie immer) Wählen Sie eine „Basis“ und messen Sie die Höhe senkrecht zu dieser Basis von der Basis zum gegenüberliegenden Scheitelpunkt.)

Trapezbereich

Verdoppeln Sie das Trapez und halbieren Sie dann den resultierenden Bereich

Wie beim Dreieck können zwei Kopien eines Trapezes zu einem Parallelogramm zusammengefügt werden.

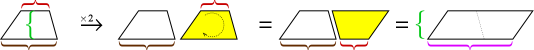
Die Höhe des Parallelogramms entspricht der Höhe des Trapezes, seine Basis ist jedoch die Summe der beiden Basen des Trapezes. Die Fläche des Parallelogramms ist also Höhe × (Basis1 + Basis2). Da es sich bei diesem Bereich jedoch um zwei Trapezoide handelt, müssen wir ihn halbieren, um den Bereich des Trapezes zu erhalten.

Präparieren des Trapezes

Wir könnten das Trapez auch so sezieren, wie wir es seziert haben das Dreieck, mit einer einzelnen Scheibe, die seine Höhe halbiert. Die beiden Teile passen zusammen, um ein Parallelogramm zu erstellen, dessen Basis die Summe der beiden Basen des Trapezes ist, dessen Höhe jedoch die Hälfte der Höhe des Trapezes beträgt.

Im Fall des Trapezes können die Basen nicht nach Belieben gewählt werden. Die beiden parallelen Seiten sind die Basen, und die Höhe ist wie immer der senkrechte Abstand von einer Basis zur gegenüberliegenden.

Die Fläche dieses Parallelogramms ist seine Höhe (halbe Höhe des Trapezes) multipliziert mit seiner Basis (Summe der Basen des Trapezes), daher ist seine Fläche die halbe Höhe × (Basis1 + Basis2). Da das Parallelogramm aus genau dem gleichen „Material“ wie das Trapez besteht, ist dies auch die Fläche des Trapezes.

In beiden Fällen ist die Fläche des Trapezes × Höhe × (Basis1 + Basis2).

Fläche anderer spezieller Vierecke

Fläche der Raute

Die Fläche einer Raute kann durch Schneiden und Neuanordnen der Teile zu einem Parallelogramm ermittelt werden. Dies kann auf verschiedene Arten erfolgen:

1. Schneiden Sie die kürzere Diagonale (a) durch, um zwei kongruente Dreiecke zu bilden. Bewegen Sie die untere Hälfte des Dreiecks neben die obere Hälfte, um ein Parallelogramm zu erstellen. Die kürzere Diagonale (a) wird zur Basis des Parallelogramms, und die Hälfte der längeren Diagonale (b) wird zur Höhe des Parallelogramms. Somit ist die Fläche der Raute a * b oder das Produkt der Diagonalen, was die Standardformel für Raute ist.
2. Eine andere ähnliche Methode besteht darin, die Raute in vier kongruente Dreiecke zu schneiden und sie zu einem Rechteck mit der kürzeren Diagonale als Basis und der halben längeren Diagonale als Höhe neu anzuordnen.
3. Nach dem Schneiden Mit der Raute in zwei kongruente Dreiecke können wir die Fläche eines der Dreiecke berechnen, nämlich * base (a) * height ( b) = ab. Dann multiplizieren Sie mit zwei, da es zwei davon gibt: 2 * ab = ab.

Drachenfläche

Die Drachenfläche ähnelt der Fläche einer Raute. Wenn Sie die längere Diagonale durchschneiden, erhalten Sie zwei kongruente Dreiecke. Wenn wir sie neu anordnen, können wir ein Parallelogramm mit der längeren Diagonale (b) als Basis und der Hälfte der kürzeren Diagonale (a) als Höhe bilden. Der Bereich wird also zu b * a = ab. Ein komplizierterer Ansatz beinhaltet ein bisschen Algebra. Schneiden Sie den Drachen über die kürzere Diagonale, um zwei Dreiecke mit der kürzeren Diagonale (a) als Basis zu bilden. Somit ist die Fläche des ersten Dreiecks a * squiggly, wobei squiggly die Höhe ist. Die Fläche des zweiten Dreiecks ist a * (b – schnörkellos), wobei (b – schnörkellos) der verbleibende Teil der längeren Diagonale ist. Die Gesamtfläche wird somit ( a * squiggly) + ( a * (b – squiggly)). Wenn wir a herausrechnen, haben wir a (squiggly + b – squiggly) = ab.

Nun, was weißt du? Grundsätzlich müssen Sie nur die Formel für den Bereich eines Parallelogramms kennen und dann die Formel für die anderen ableiten.