방법 : 유리 함수가 주어지면 그래프의 수직 점근선을 식별합니다.

1. 분자와 분모.
2. 함수 영역의 제한 사항에 유의하세요.
3. 분자와 분모의 공약수를 취소하여 식을 줄입니다.
4. 모든 값을 기록해 둡니다. 이 단순화 된 버전에서는 분모가 0이됩니다. 수직 점근선이 발생하는 곳입니다.
5. 점근선이 발생하지 않는 도메인의 모든 제한 사항에 유의하십시오. 제거 가능한 불연속성입니다.

f \ left (x \ right) = \ frac {\ left (x + 1 \ right) \ left (x -1 \ 오른쪽)} {\ left (x + 1 \ 오른쪽) \ left (x-3 \ 오른쪽)}

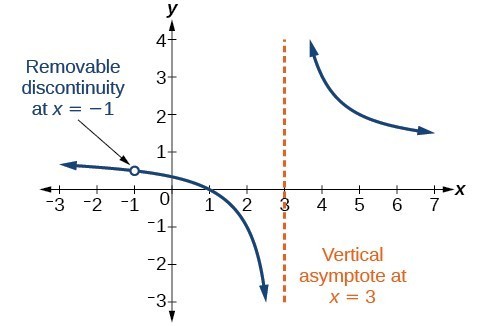
그림 10

일반 참고 사항 : 합리적 함수의 제거 가능한 불연속성

합리적 함수의 그래프에서 제거 가능한 불연속성 발생 x = a에서 a가 분자의 요소와 공통 인 분모의 요소에 대해 0이면. 분자와 분모를 인수 분해하고 공약수를 확인합니다. 발견되면 공약수를 0으로 설정하고 해결합니다. 이것은 이동식 불연속의 위치입니다. 이 인수의 다중도가 분모의 다중도보다 크거나 같은 경우에 해당됩니다. 이 요소의 다중도가 분모에서 더 크면 해당 값에 여전히 점근선이 있습니다.

\ text {예 :} f \ left (x \ right) = \ frac {4x + 2} {{x} ^ {2} + 4x-5}

\ text {예 :} f \ left (x \ right) = \ frac {3 {x} ^ {2} -2x + 1} {x-1}

\ text {예 :} f \ left (x \ right) = \ frac {3 {x} ^ {2} +2} {{x} ^ {2 } + 4x-5}

f \ left (x \ right) = \ frac {3 {x} ^ {5}-{x} ^ { 2}} {x + 3}

f \ left (x \ right) \ approx \ frac {3 {x } ^ {5}} {x} = 3 {x} ^ {4},

x \ to \ pm \ infty, f \ left (x \ right) \ to \ infty

A General Note : 수평 점근선 유리 함수

유리 함수의 수평 점근선은 분자와 분모의 각도를 보면 알 수 있습니다.

• 분자의 각도는 분모의 각도보다 작습니다. y = 0에서 수평 점근선.
• 분자의 정도가 분모의 정도보다 1만큼 큽니다. 수평 점근선 없음; 경사 점근선.
• 분자의 정도는 분모의 정도와 같습니다 : 선행 계수의 비율에서 수평 점근선.

일반 참고 사항 : 유리 함수의 절편

유리 함수는 입력이 0 일 때 y 절편을 갖습니다. 함수는 0에서 정의됩니다. 합리적 함수는 함수가 0에서 정의되지 않은 경우 y 절편을 갖지 않습니다.

마찬가지로 유리수 함수는 출력이 0이되도록하는 입력에서 x 절편을 갖습니다. 분수는 분자가 0 일 때만 0과 같으므로 x 절편은 유리 함수의 분자가 0 일 때만 발생할 수 있습니다.

Try It 7

오른쪽으로 3 단위, 아래로 4 단위 이동하는 역 제곱 함수를 고려하여이 함수를 유리 함수로 작성하십시오. 그런 다음 x- 및 y- 절편과 수평 및 수직 점근선을 찾으십시오.

해결책