지수 분포
Marco Taboga, PhD
지수 분포는 다음에 사용되는 연속 확률 분포입니다. 주어진 이벤트가 발생하기 전에 기다려야하는 시간을 모델링합니다. 이것은 기하 분포의 연속적인 대응이며, 대신 이산입니다.
때로는 음의 지수 분포라고도합니다.

소개
특정 지역에서 지진이 발생하기까지 시간이 얼마나 걸리나요? 고객이 매장에 들어올 때까지 얼마나 기다려야합니까? 콜센터가 다음 전화를 받기까지 얼마나 걸리나요? 기계 조각이 무너지지 않고 얼마나 오래 작동할까요?
이와 같은 질문은 지수 분포를 사용하여 확률 적으로 자주 답변됩니다.
이 모든 질문은 필요한 시간과 관련이 있습니다. 주어진 이벤트가 발생하기 전에 기다립니다. 이 대기 시간을 알 수없는 경우 지수 분포를 갖는 임의의 변수로 생각하는 것이 적절합니다.
대략적으로 말하면 필요한 시간  특정 시간 간격 동안 이벤트가 발생할 확률이 해당 시간 간격의 길이에 비례하는 경우 이벤트가 발생하기 전에 대기하는 것은 지수 분포를 갖습니다.
특정 시간 간격 동안 이벤트가 발생할 확률이 해당 시간 간격의 길이에 비례하는 경우 이벤트가 발생하기 전에 대기하는 것은 지수 분포를 갖습니다.
보다 정확하게는 
이 시간 사이에 구성된 시간 간격의 길이  에 대략적으로 비례하는 경우
에 대략적으로 비례하는 경우
에는 지수 분포가 있습니다.  및
및  , 모든 시간 인스턴트
, 모든 시간 인스턴트  .
.
많은 실제 상황에서이 속성은 매우 현실적입니다. 이것이 지수 분포가 대기 시간을 모델링하는 데 널리 사용되는 이유입니다.
지수 분포는 포아송 분포와 엄격하게 관련됩니다. 1) 이벤트가 두 번 이상 발생할 수 있고 2) 두 번의 연속 발생 사이에 경과 된 시간이 기하 급수적으로 분포되고 이전 발생과 독립적 인 경우 주어진 시간 단위 내에서 이벤트 발생 횟수는 포아송 분포를 갖습니다. 이 사실에 대한보다 자세한 설명과 직관적 인 그래픽 표현을 위해 독자에게 푸 아송 분포에 대한 강의를 보도록 초대합니다.
정의
지수 분포는 다음과 같은 특징이 있습니다.
정의  를 연속 랜덤 변수로 지정합니다. 양의 실수 집합을 지원하도록합니다 :
를 연속 랜덤 변수로 지정합니다. 양의 실수 집합을 지원하도록합니다 : 
 .
.  는 확률 밀도 함수가
는 확률 밀도 함수가
 매개 변수를 비율 매개 변수라고합니다.
매개 변수를 비율 매개 변수라고합니다.
지수 분포를 갖는 랜덤 변수를 지수 랜덤 변수라고도합니다.
다음은  은 합법적 인 확률 밀도 함수입니다.
은 합법적 인 확률 밀도 함수입니다.
음이 아닌 것은 분명합니다.  에 대한
에 대한  의 적분이
의 적분이  와 같다는 것을 증명해야합니다. 이는 다음과 같이 증명됩니다.
와 같다는 것을 증명해야합니다. 이는 다음과 같이 증명됩니다. 
지수 분포를 더 잘 이해하기 위해 밀도 플롯을 살펴볼 수 있습니다.
속도 매개 변수 및 해석
두 날짜  및
및  는
는  에 비례합니다 (
에 비례합니다 ( 이전에 발생하지 않은 정보에 따라). 비율 매개 변수
이전에 발생하지 않은 정보에 따라). 비율 매개 변수  는 비례 상수입니다.
는 비례 상수입니다.  여기서
여기서  는
는  보다 높은 차수 (즉,
보다 높은 차수 (즉,  의 함수) > 않습니다).
의 함수) > 않습니다).
위의 비례 조건은 지수 분포를 완전히 특성화하기에 충분합니다.
명제 비례 조건  은
은  에 지수 분포가있는 경우에만 충족됩니다.
에 지수 분포가있는 경우에만 충족됩니다.
조건부 확률  는 다음과 같이 작성할 수 있습니다.
는 다음과 같이 작성할 수 있습니다. 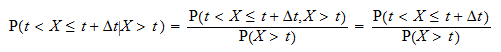
 는
는  의 분포 함수, 즉
의 분포 함수, 즉  및
및  생존 함수 :
생존 함수 :  그런 다음
그런 다음  양변을
양변을  ,
,  여기서
여기서  는
는 
 가
가  인 경향이 있습니다. 양쪽에 제한을두면
인 경향이 있습니다. 양쪽에 제한을두면  또는 미분의 정의에 의해 다음을 얻습니다.
또는 미분의 정의에 의해 다음을 얻습니다.  이 미분 방정식은 체인을 사용하여 쉽게 풀 수 있습니다. 규칙 :
이 미분 방정식은 체인을 사용하여 쉽게 풀 수 있습니다. 규칙 :  양변의
양변의  에서
에서  까지 적분을 취하면
까지 적분을 취하면  및
및  또는
또는  하지만
하지만  (
( 는 음수 값을 가질 수 없기 때문에)는
는 음수 값을 가질 수 없기 때문에)는  양쪽을 확장하면
양쪽을 확장하면  를 얻습니다. 따라서
를 얻습니다. 따라서  또는
또는  하지만 밀도 함수는 분포 함수의 1 차 도함수입니다.
하지만 밀도 함수는 분포 함수의 1 차 도함수입니다.  그리고 가장 오른쪽 항은 지수 랜덤 변수의 밀도입니다. 따라서 비례 조건은
그리고 가장 오른쪽 항은 지수 랜덤 변수의 밀도입니다. 따라서 비례 조건은  가 지수 랜덤 변수 인 경우에만 충족됩니다.
가 지수 랜덤 변수 인 경우에만 충족됩니다.
예상 값
지수 랜덤 변수  의 예상 값은
의 예상 값은 
다음과 같이 파생 될 수 있습니다. 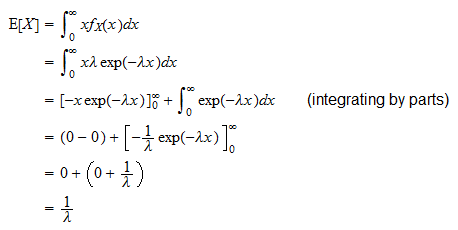
분산
지수 랜덤 변수  는
는 
It입니다. 일반적인 분산 공식 ( )을 통해 파생 될 수 있습니다.
)을 통해 파생 될 수 있습니다. 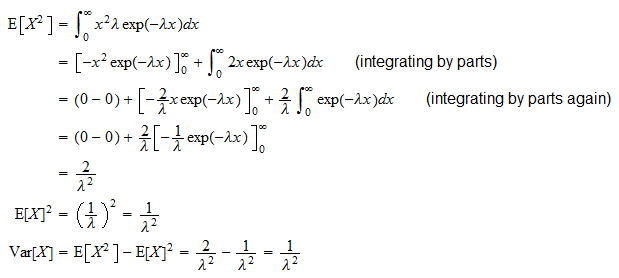
모멘트 생성 함수
지수 랜덤 변수의 모멘트 생성 함수  는 모든
는 모든  에 대해 정의됩니다.
에 대해 정의됩니다. 
모멘트 생성 함수의 정의는  의 물론 위의 적분은
의 물론 위의 적분은  , 즉
, 즉  인 경우에만 수렴됩니다. 따라서 모든
인 경우에만 수렴됩니다. 따라서 모든  에 대해 지수 랜덤 변수의 모멘트 생성 함수가 존재합니다.
에 대해 지수 랜덤 변수의 모멘트 생성 함수가 존재합니다.
특성 함수
지수 랜덤 변수  의 특성 함수는
의 특성 함수는 
특성 함수의 정의와  우리가 작성할 수 있다는 사실을 사용하여
우리가 작성할 수 있다는 사실을 사용하여  이제 두 적분을 개별적으로 계산합니다. . 첫 번째 적분은
이제 두 적분을 개별적으로 계산합니다. . 첫 번째 적분은 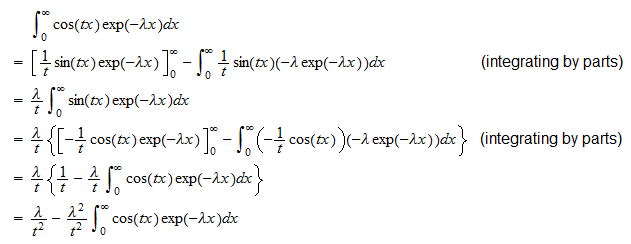 따라서
따라서  다시 정렬하여
다시 정렬하여  또는
또는  두 번째 적분은
두 번째 적분은 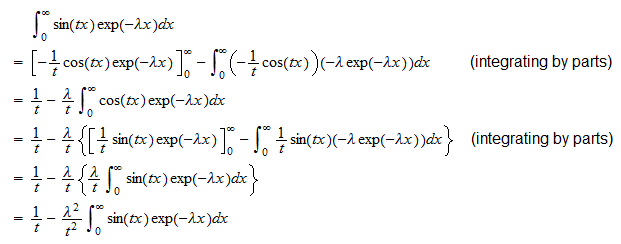 따라서
따라서  다시 정렬하여
다시 정렬하여  또는
또는  조각을 모아서
조각을 모아서 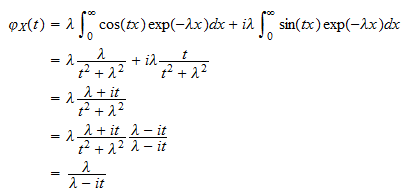
분포 함수
지수 랜덤 변수  의 분포 함수는
의 분포 함수는 
 이면
이면 
 는 음수 값을 사용할 수 없습니다.
는 음수 값을 사용할 수 없습니다.  인 경우
인 경우 
세부 정보
다음 하위 섹션에서 지수 분포에 대한 자세한 내용을 확인할 수 있습니다.
메모리리스 속성
지수 분포의 가장 중요한 속성 중 하나는 메모리리스 속성입니다.  모든
모든  .
.
이것은 다음과 같이 증명됩니다. 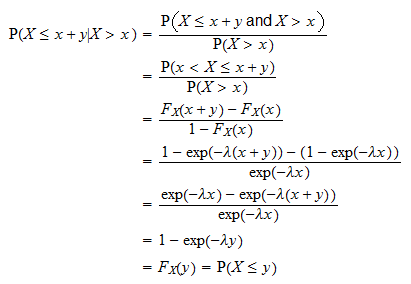
 는 특정 이벤트 전에 기다려야하는 시간입니다. 발생합니다. 위의 속성은
는 특정 이벤트 전에 기다려야하는 시간입니다. 발생합니다. 위의 속성은  길이의 시간 간격 동안 이벤트가 발생할 확률은 이미 경과 된 시간 (
길이의 시간 간격 동안 이벤트가 발생할 확률은 이미 경과 된 시간 ( ).
).
지수 랜덤 변수의 합은 감마 랜덤 변수입니다.
 , , …,
, , …,  는
는  매개 변수가
매개 변수가  인 지수 분포를 갖는 상호 독립적 인 랜덤 변수입니다.
인 지수 분포를 갖는 상호 독립적 인 랜덤 변수입니다.
p>
Define 
그런 다음 합계  는 매개 변수가
는 매개 변수가  및
및  .
.
모멘트를 사용하여 증명되었습니다. 함수 생성 (상호 독립적 인 랜덤 변수의 합계의 모멘트 생성 함수는 모멘트 생성 함수의 곱일뿐임을 기억하십시오) :  후자는 감마의 모멘트 생성 함수입니다. 매개 변수
후자는 감마의 모멘트 생성 함수입니다. 매개 변수  및
및  를 사용한 분포. 따라서
를 사용한 분포. 따라서  에는 감마 분포가 있습니다. 두 개의 임의 변수가 동일한 모멘트 생성 함수를 가질 때 동일한 분포를 갖기 때문입니다.
에는 감마 분포가 있습니다. 두 개의 임의 변수가 동일한 모멘트 생성 함수를 가질 때 동일한 분포를 갖기 때문입니다.
랜덤 변수  도 때때로 Erlang 분포를 가지고 있다고합니다. Erlang 분포는 감마 분포의 특별한 경우 일뿐입니다. 감마 확률 변수는 지수 확률 변수의 합계로 쓸 수있는 경우 Erlang 확률 변수이기도합니다.
도 때때로 Erlang 분포를 가지고 있다고합니다. Erlang 분포는 감마 분포의 특별한 경우 일뿐입니다. 감마 확률 변수는 지수 확률 변수의 합계로 쓸 수있는 경우 Erlang 확률 변수이기도합니다.
밀도 플롯
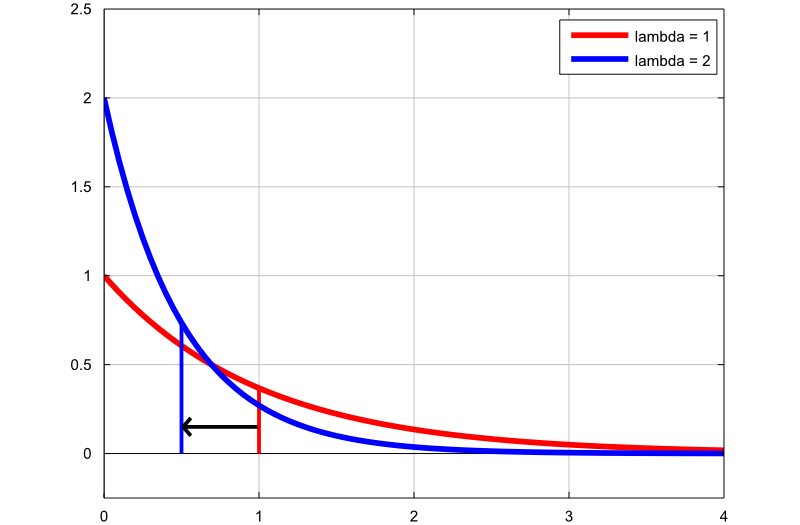
다음 플롯은 비율 매개 변수를 변경하여 지수 분포의 밀도가 어떻게 변하는 지 보여줍니다.
-
첫 번째 그래프 (빨간색 선)는 지수 랜덤 변수의 확률 밀도 함수입니다. 요율 매개 변수
 포함;
포함; -
두 번째 그래프 (파란색 선)는 비율 매개 변수가
 인 지수 랜덤 변수의 확률 밀도 함수입니다.
인 지수 랜덤 변수의 확률 밀도 함수입니다.
가는 수직선은 두 분포의 평균을 나타냅니다. 요율 매개 변수를 늘리면 분포 평균이  에서
에서  로 감소합니다.
로 감소합니다.
해결 된 연습
아래에서 솔루션을 설명하는 몇 가지 연습을 찾을 수 있습니다.
연습 1
 를 매개 변수
를 매개 변수  가있는 지수 랜덤 변수로 지정합니다. 다음 확률을 계산합니다.
가있는 지수 랜덤 변수로 지정합니다. 다음 확률을 계산합니다. 
우선 확률을 다음과 같이 쓸 수 있습니다.  연속 랜덤 변수가 특정 값을 취할 확률이 0과 같다는 사실을 사용합니다 (연속 랜덤 변수 및 0 확률 이벤트 참조). 이제 확률은
연속 랜덤 변수가 특정 값을 취할 확률이 0과 같다는 사실을 사용합니다 (연속 랜덤 변수 및 0 확률 이벤트 참조). 이제 확률은  의 분포 함수 측면에서 다음과 같이 쓸 수 있습니다.
의 분포 함수 측면에서 다음과 같이 쓸 수 있습니다. 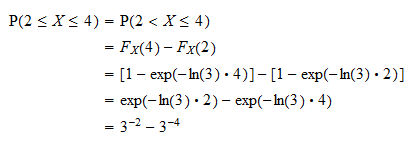
연습 2
랜덤 변수  에 매개 변수가
에 매개 변수가  인 지수 분포가 있다고 가정합니다. 다음 확률을 계산합니다.
인 지수 분포가 있다고 가정합니다. 다음 확률을 계산합니다. 
이 확률은
: 
연습 3
랜덤 변수가  에 매개 변수가
에 매개 변수가  인 지수 분포가있는 경우
인 지수 분포가있는 경우  가 예상 값보다 작습니다. ?
가 예상 값보다 작습니다. ?
 매개 변수가있는 지수 랜덤 변수의 예상 값은
매개 변수가있는 지수 랜덤 변수의 예상 값은  위의 확률은
위의 확률은  :
: 
의 분포 함수를 사용하여 계산할 수 있습니다. h2> 인용 방법
인용 :