푸 아송 분포
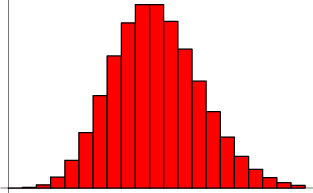
푸 아송 과정을 고려할 때 
시행에서 정확히 
번 성공할 확률은 이항 분포의 한계로 주어집니다.
 |
(1)
|
예상 성공 횟수의 함수로 분포보기
 |
(2)
|
샘플 크기 고정 
, 방정식 (2)는 다음이됩니다.
 |
(3)
|
샘플 크기 
가 커지면 분포가 다가옵니다.
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
Poisson 분포 (Papoulis 1984, pp. 101 및 554; Pfeiffer and Schum 1973, p. 200). 샘플 크기 
는 확률 함수에서 완전히 삭제되었으며 
의 모든 값에 대해 동일한 함수 형식을가집니다.
Poisson 분포는 WolframLanguage에서 PoissonDistribution으로 구현됩니다.
예상대로 Poisson 분포는 확률의 합이 1이되도록 정규화됩니다.
 |
(9 )
|
확률 비율은 다음과 같이 지정됩니다.
 |
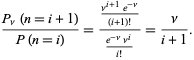(10)
|
푸 아송 분포가 최대 값에 도달하는 경우
 |
(11)
|
여기서 는 Euler-Mascheroni 상수이고 
는 초월 방정식으로 이어지는 조화 수입니다.
 |
(12)
|
의 경우 정확히 해결할 수 없습니다.
푸 아송 분포의 모멘트 생성 함수는 다음과 같이 제공됩니다.
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
그래서
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, p. 554).
원시 모멘트는 합산에 의해 직접 계산 될 수도 있습니다. 이는 Bell 다항식 
및 두 번째 종류의 스털링 수와 예상치 못한 연결을 생성합니다.
 |
(21)
|
Dobiński의 공식이라고합니다.따라서
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
중심 모멘트는 다음과 같이 계산 될 수 있습니다.
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
평균, 분산, 왜도 및 첨도 초과는
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
푸 아송 분포의 특성 함수는 다음과 같습니다.
(Papoulis 1984, pp. 154 및 554), 누적 생성 함수는 다음과 같습니다. / p>
 |
(34)
|
그래서
 |
(35)
|
푸 아송 분포의 평균 편차는 다음과 같습니다.
 |
(36)
|
푸 아송 분포는 다음과 같이 표현할 수도 있습니다.
 |
(37)
|
 |
(38)
|
두 변수에서 aPoisson 분포의 모멘트 생성 함수는 다음과 같습니다.
 |
(39)
|
독립 변수 
, 
, …, 
에는 매개 변수가 
, 
, … 인 포아송 분포가 있습니다., 
다음에
 |
(40)
|
매개 변수가있는 포아송 분포가 있습니다.
 |
(41)
|
누적 생성 함수가 다음과 같기 때문에 알 수 있습니다.
 |
(42)
|
 |
(43)
|
Saslaw (1989)는 모델링을 위해 Poisson 분포의 일반화를 사용했습니다. 우주에서 관측 된 은하 군집. 이 배포 형식은
 |
(44)
|
여기서 
는 볼륨 
, 
, 는 은하의 평균 밀도이고 
, 
는 중력 에너지와 운동 에너지의 비율입니다. 독특한 동작의 에너지, 
는
 |
(45)
|
실제로 
가 포함 된 Poisson 배포판입니다. 마찬가지로 
는 
를 제공합니다.