方法：有理関数を指定して、グラフの垂直方向の無症状を特定します。

1. 分子と因子分母。
2. 関数のドメインの制限に注意してください。
3. 分子と分母の共通の因数をキャンセルして、式を減らしてください。
4. 値に注意してください。これにより、この簡略化されたバージョンでは分母がゼロになります。これらは、垂直方向の漸近線が発生する場所です。
5. 漸近線が発生しないドメイン内の制限に注意してください。これらは除去可能な不連続性です。

f \ left（x \ right）= \ frac {\ left（x + 1 \ right）\ left（x -1 \ right）} {\ left（x + 1 \ right）\ left（x-3 \ right）}

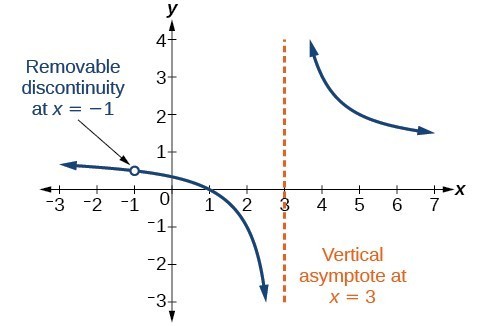
図10

一般的な注意：有理関数の除去可能な不連続性

有理関数のグラフで除去可能な不連続性が発生しますx = aで、分子の因子と共通の分母の因子のaがゼロの場合。分子と分母を因数分解し、共通の因数をチェックします。見つかった場合は、公約数を0に設定して解きます。これは、取り外し可能な不連続部の場所です。これは、この係数の多重度が分母の多重度以上の場合に当てはまります。この係数の多重度が分母の方が大きい場合でも、その値には漸近線があります。

\ text {例：} f \ left（x \ right）= \ frac {4x + 2} {{x} ^ {2} + 4x-5}

\ text {例：} f \ left（x \ right）= \ frac {3 {x} ^ {2} -2x + 1} {x-1}

\ text {例：} f \ left（x \ right）= \ frac {3 {x} ^ {2} + 2} {{x} ^ {2 } + 4x-5}

f \ left（x \ right）= \ frac {3 {x} ^ {5}-{x} ^ { 2}} {x + 3}

f \ left（x \ right）\ approx \ frac {3 {x } ^ {5}} {x} = 3 {x} ^ {4}、

x \ to \ pm \ infty、f \ left（x \ right）\ to \ infty

一般的な注意：水平方向の漸近線有理関数

有理関数の水平方向の漸近線は、分子と分母の次数を調べることで決定できます。

• 分子の次数は、分母の次数よりも小さくなります。 y = 0での水平方向の漸近線。
• 分子の次数が分母の次数より1大きい：水平方向の漸近線なし。傾斜した漸近線。
• 分子の次数は分母の次数に等しい：先行係数の比率での水平方向の漸近線。

一般的な注意：有理関数の切片

入力がゼロの場合、有理関数はy切片を持ちます。 関数はゼロで定義されます。 関数がゼロで定義されていない場合、有理関数にはy切片がありません。

同様に、有理関数には入力にx切片があり、出力がゼロになります。 分数は分子がゼロの場合にのみゼロに等しいため、x切片は、有理関数の分子がゼロに等しい場合にのみ発生します。

試してみてください7

右に3単位、下に4単位シフトされる逆数二乗関数を前提として、これを有理関数として記述します。 次に、x切片とy切片、および水平方向と垂直方向の漸近線を見つけます。

解決策