指数分布
マルコタボガ博士
指数分布は、次の目的で使用される連続確率分布です。特定のイベントが発生するまで待機する必要がある時間をモデル化します。これは、幾何分布の連続的な対応物であり、代わりに離散的です。
負の指数分布とも呼ばれます。
はじめに
特定の地域で地震が発生するまでにどのくらいの時間がかかりますか？お客様が当店に入るまでどのくらい待つ必要がありますか？コールセンターが次の電話を受けるまでどのくらいかかりますか？機械が故障することなくどのくらいの期間機能しますか？
このような質問は、指数分布を使用して確率的に回答されることがよくあります。
これらの質問はすべて、必要な時間に関するものです。特定のイベントが発生する前に待機します。この待機時間が不明な場合は、指数分布の確率変数と考えるのが適切な場合がよくあります。
大まかに言えば、必要な時間
イベントが発生する前に待機することは、特定の時間間隔中にイベントが発生する確率がその時間間隔の長さに比例する場合、指数分布になります。
より正確には、は、条件付き確率が時間の間に含まれる時間間隔の長さにほぼ比例する場合、指数分布になります。 および、いつでも。
多くの実際的な状況では、このプロパティは非常に現実的です。これが、待機時間をモデル化するために指数分布が非常に広く使用されている理由です。
指数分布は、ポアソン分布と厳密に関連しています。 1）イベントが複数回発生する可能性があり、2）2つの連続する発生間の経過時間が指数分布し、前の発生とは無関係である場合、特定の時間単位内のイベントの発生数はポアソン分布になります。この事実のより詳細な説明と直感的なグラフ表現については、ポアソン分布に関する講義をご覧になることをお勧めします。
定義
指数分布の特徴は次のとおりです。
定義を連続確率変数とします。そのサポートを正の実数のセットとします： とします。 は、確率密度関数が
の指数分布を持つと言います。
パラメータはレートパラメータと呼ばれます。
指数分布を持つ確率変数は、指数確率変数とも呼ばれます。
以下は、は正当な確率密度関数です。
非負性は明らかです。 との積分がに等しいことを証明する必要があります。これは次のように証明されます。
指数分布をよりよく理解するために、密度プロットを見ることができます。
レートパラメータとその解釈
イベントが2つの日付とはに比例します（より前に発生していないという情報を条件とします）。レートパラメータは、比例定数です。ここで、はの極小値です。 よりも高次（つまり、よりも早くゼロになるの関数>します。
上記の比例条件は、指数分布を完全に特徴付けるのにも十分です。
提案比例条件は、に指数分布がある場合にのみ満たされます。
条件付き確率は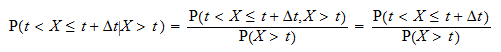
の分布関数、つまりそしてその生存関数：次に、両側を、を取得します。ここで、は がになる傾向がある場合。両側を制限すると、が得られます。または、導関数の定義により、次のようになります。この微分方程式は、チェーンを使用して簡単に解くことができますルール：両側のからへの積分を取ると、およびまたはただし、 （は負の値を取ることができないため）は、両側を指数化すると、が得られます。したがって、またはただし、密度関数は分布関数の一次導関数です：そして右端の項は指数ランダム変数の密度です。したがって、が指数ランダム変数である場合にのみ比例条件が満たされます
期待値
指数ランダム変数の期待値は
次のように導出できます。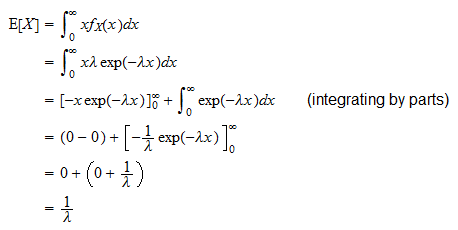
分散
指数ランダム変数は
It通常の分散式（）のおかげで導出できます：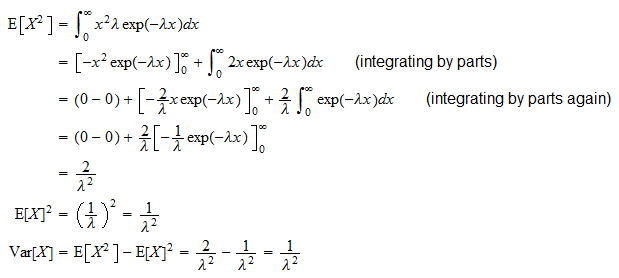
モーメント母関数
指数ランダム変数のモーメント母関数は、任意のに対して定義されています：
モーメント母関数の定義によりのもちろん、上記の積分はの場合、つまりの場合にのみ収束します。したがって、指数ランダム変数のモーメント母関数は、すべてのに存在します。
特性関数
指数ランダム変数の特性関数は
特性関数の定義と、を記述できるという事実を使用することで 2つの積分を別々に計算します。 。最初の積分は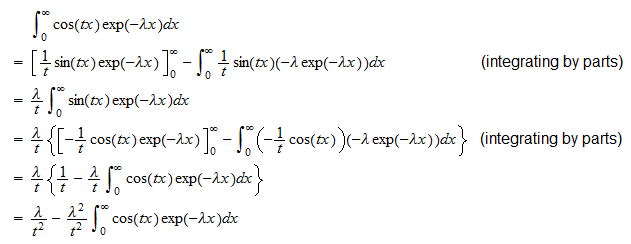
したがって、再配置してまたは 2番目の積分は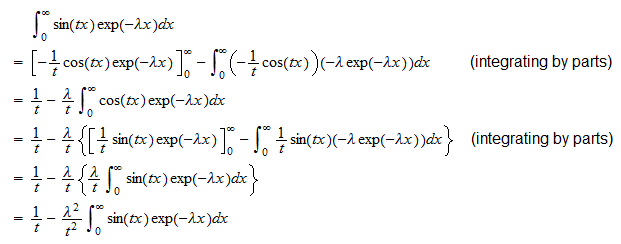
したがって、これを再配置してまたはピースを組み合わせると、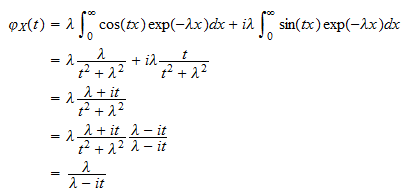
<が得られます。 / div>
分布関数
指数ランダム変数の分布関数は
の場合、はは負の値を取ることはできません。 の場合、
詳細
次のサブセクションでは、指数分布の詳細を確認できます。
メモリレスプロパティ
指数分布の最も重要なプロパティの1つは、メモリレスプロパティです。任意の。
これは次のように証明されます。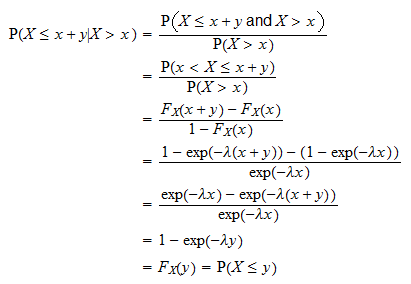 
は、特定のイベントの前に待機する必要がある時間です発生します。上記のプロパティは、イベントが長さの時間間隔中に発生する確率は、すでに経過した時間とは無関係であることを示しています（）イベントが発生しない。
指数確率変数の合計はガンマ確率変数です
、、..。、は相互に独立した確率変数であり、パラメーターで指数分布します。
定義
次に、合計は、パラメーター
および。
これはモーメントを使用して証明されます生成関数（相互に独立した確率変数の合計のモーメント生成関数は、それらのモーメント生成関数の積にすぎないことに注意してください）：後者はガンマのモーメント生成関数です。パラメータおよびを使用した分布。したがって、にはガンマ分布があります。これは、2つの確率変数が同じモーメント母関数を持っている場合、同じ分布を持つためです。
確率変数は、アーラン分布を持っていると言われることもあります。 Erlang分布は、ガンマ分布の特殊なケースです。ガンマ確率変数は、指数確率変数の合計として記述できる場合、Erlang確率変数でもあります。
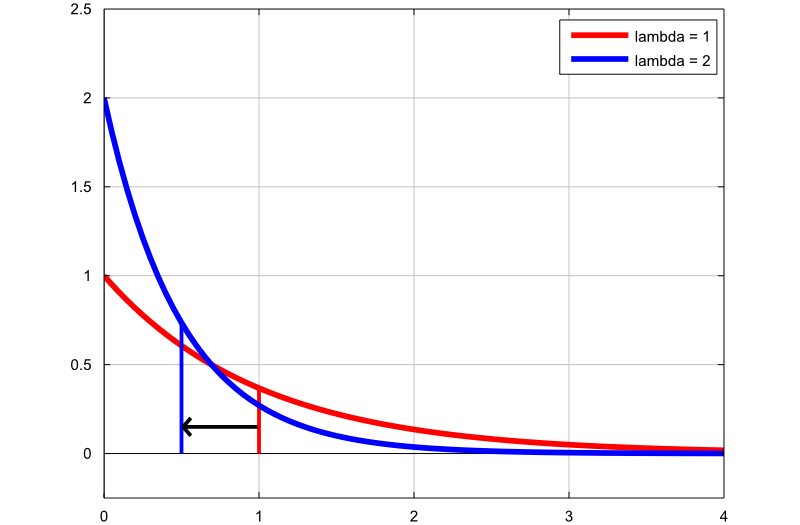
密度プロット
次のプロットは、レートパラメーターを変更することによって指数分布の密度がどのように変化するかを示しています。
-
最初のグラフ（赤い線）は、指数確率変数の確率密度関数です。レートパラメータ
; -
2番目のグラフ（青い線）は、レートパラメーター
を持つ指数確率変数の確率密度関数です。
細い垂直線は、2つの分布の平均を示します。レートパラメータを増やすことにより、分布の平均をからに減らすことに注意してください。
解決済みの演習
以下に、説明された解決策を含むいくつかの演習を示します。
演習1
をパラメーターを持つ指数ランダム変数とします。次の確率を計算します。
まず、確率を連続確率変数が特定の値をとる確率がゼロに等しいという事実を使用します（連続確率変数とゼロ確率イベントを参照）。これで、確率はの分布関数で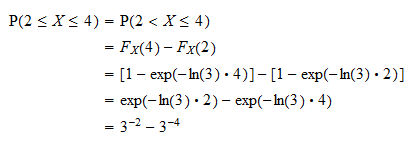
と書くことができます。演習2
確率変数にパラメーターの指数分布があるとします。次の確率を計算します。
この確率は、
：
演習3
確率変数の確率はどれくらいですかにパラメーターの指数分布がある場合、は期待値よりも小さくなります。 ？
パラメーターを持つ指数確率変数の期待値は上記の確率は、：
<の分布関数を使用して計算できます。 h2>引用方法
次のように引用してください：