大学代数

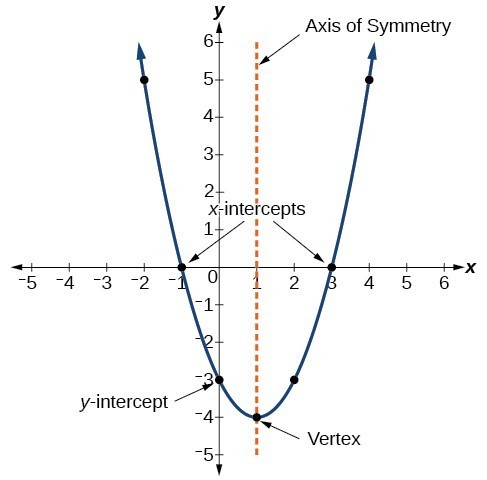
2次関数のグラフは、パラボラと呼ばれるU字型の曲線です。グラフの重要な特徴の1つは、頂点と呼ばれる極値点があることです。放物線が開いた場合、頂点はグラフの最低点、つまり2次関数の最小値を表します。放物線が開いた場合、頂点はグラフの最高点、つまり最大値を表します。いずれの場合も、頂点はグラフのターニングポイントです。グラフは、対称軸と呼ばれる、頂点を通る垂直線で対称にもなります。

二次関数の方程式

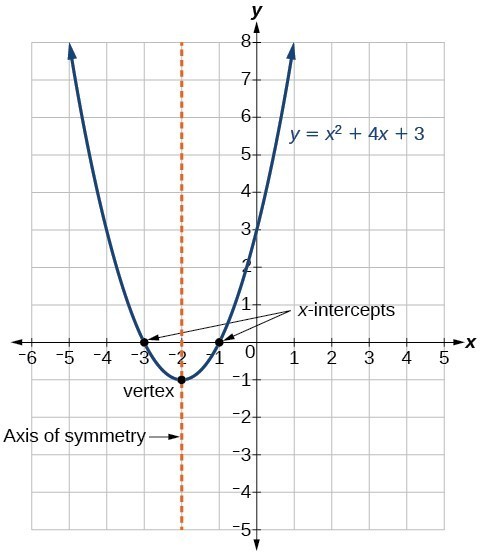
2次関数の一般的な形式は、関数を次の形式で表します

f \ left（x \ right）= a {x} ^ {2} + bx + c

2次関数の標準形式は、関数を次の形式で表します

f \ left（x \ right）= a {\ left（xh \ right）} ^ {2} + k

一般に2次関数を指定フォーム、放物線の頂点を見つけます。

放物線の頂点を特定したい理由の1つは、この点が出力の最大値または最小値kが発生する場所、および場所を通知することです。それが発生します、h。二次関数の一般的な形式が与えられた場合：

f（x）= ax ^ 2 + bx + c

定義できます頂点（h、k）は、次のようにします。

二次関数のドメインと範囲の検索

任意の数値を二次関数の入力値にすることができます。したがって、2次関数の定義域はすべて実数です。放物線は頂点に最大値または最小値があるため、範囲が制限されます。放物線の頂点は最大または最小のいずれかになるため、範囲は、頂点のy座標以上または転換点のy座標以下のすべてのy値で構成されます。 、放物線が開くか下がるかによって異なります。

貢献してください！

このページを改善する詳細