測定：面積の数式を見つける
面積の数式
面積が「2-Dの量」であるという非公式な概念を持っている学生地域内に含まれる「もの」は、単に暗記するように求められることが多い式のほとんどを自分で発明することができます。彼らが再発明する各式は、彼らが知っている他の式に対する理解（および記憶）を強化するのに役立ちます。 （表面積も参照してください。）
長方形の面積
面積の単位として正方形を選択することにより、長方形の面積について直感的に理解できます。この正方形
の面積が1であると判断した場合、7倍の長さの長方形
は7×1になります。面積として。
の2倍の高さの長方形は、その面積が2倍になるため、
は2×7単位の面積です。 7つの正方形の2つの行を数えることができます。同様に、
には7つの正方形が3行（または3つの正方形が7列）あり、合計で7×3の正方形であるため、面積は21平方単位になります。
1行の正方形の数は、長方形の長さです。行数は長方形の高さです。したがって、面積は長さ×高さです。
長方形は斜めに描くことができるため、「高さ」は「底辺に垂直な方向」を意味すると定義され、「底辺」は次のように定義されます。
これは、数を数えるために機能します。分数に対しても機能します。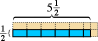
ここに示されている青い長方形の長さは半分です。長さ-高さ単位、長さ-単位幅。対応する正方形を面積単位として選択すると、青い長方形に5つの半単位の面積と1/4単位の面積が含まれていることがわかります。合計で2と3/4の面積単位。（ピンクの部分は各正方形の面積単位の完成を示します。）
すべての数値を含めるために、長方形の面積を底辺×高さとして定義します。 （ここで、「底辺」と「高さ」は、同じ単位で測定された、それらの辺の長さを意味します。）
平行四辺形の面積
アイデアを得る
平行線の面積の公式は、解剖することで理解できます。平行四辺形を作成し、パーツを再配置して長方形を作成します。平行四辺形と長方形は同じ部分で構成されているため、必然的に同じ面積になります。 （これらの領域が同じである理由の詳細については、領域の定義を参照してください。）
まったく同じベースの長さ（青）とまったく同じ高さ（緑）。底辺×高さは長方形の面積を与えるので、平行四辺形で同じ測定値を使用してその面積を計算できます：底辺×高さ。 （以前と同様に、「高さ」はベースに対して垂直に測定され、「ベース」は最初に選択した側です。平行四辺形を参照してください。）
上記のカットにより、ベースの長さが次のようになっていることが簡単にわかります。変更なし。実際、垂直カットはベースに沿ってどこでも行うことができます。
穴の拡大
直感と証明
この分析により、平行四辺形の面積式を直感的に理解できます。これは、平行四辺形が本来あるべき理由です。しかし、解剖が本当に「機能する」かどうかは疑問視していません。つまり、平行四辺形
を切り取り、その部分を再配置すると、
が得られると予想され、結果は確かにそのようになります。外観は誤解を招く可能性があります。その三角形を移動すると、結果が長方形になることを保証するものは何ですか？
に似ている場合はどうなりますか（誇張はされませんが）？結果がそうでない場合常に完全な長方形であるため、長方形の面積式の知識を使用して平行四辺形の式を作成することはできません。高校では、平行四辺形の2つの部分を適切に再組み立てすると、長方形が作成されることを証明できます。 。K-8学年では、ほとんどの場合、生徒は視覚的な実験に頼って直感的な感覚を得る必要があります。これらの解剖が機能する理由の詳細をご覧ください。
短辺をベースとして選択した場合はどうなりますか？
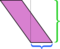
ベースとして任意の側を自由に選択できます。「高さ」と定義されていますベースとして選択した側に垂直に測定されます。短辺（青）をベースにすると、上記の解剖はそれほど説得力がありません。その高度に沿って切り取り、パーツを再配置すると、混乱が生じます。
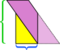
この特定の例では、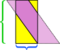 
をもう1つカットすることで混乱を救うことができますが、平行四辺形がさらに長くて細い場合はどうでしょうか。
平行四辺形は、どれだけ長くて細いかに関係なく、この方法で解剖できるため、パーツ（おそらくそれらの多く）を長方形に再配置できます。しかし、これが常に実行できることを示すには、さらに多くの作業が必要です。別のアイデアが必要です。
この場合、解剖のアイデアが少し異なると、生活がはるかに楽になります。 （自分で、元のケースでも機能することを示すことができます。）
- 平行四辺形を長方形で囲みます。
- 平行四辺形の内側にない長方形の2つの部分は、合同な三角形です。
- これらの三角形の1つを、出会って長方形を形成するまで、他の三角形に向かってスライドさせます。
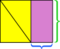外側の長方形の総面積は変更されておらず（以前と同じ長方形です）、黄色の領域は変更されていない（ピースが移動したばかり）ため、それら—紫色の領域—は同じでなければなりません。前と同じように、長方形の紫色の領域の寸法が元の平行四辺形の底辺と高さであることがわかります。
直感と証明、リプライズ：繰り返しになりますが、解剖は本質的な洞察を提供しますが、長方形を作るために一緒にフィットしているように見える2つの黄色の三角形が、ほぼ正確にフィットすることを保証するには、もう少し作業が必要です。
なぜそんなに注意することが重要なのですか？
他の面積式（下記）を作成するときは、平行四辺形の面積を見つける方法を使用したいので、私たちが見つけたルールに頼ることができるように。パーツを再配置しても面積が変わらないことは確かです。つまり、結局のところ、面積の定義方法です。ただし、パーツが主張どおりに組み合わされていることも確認する必要があります。そうしないと、行った測定に頼ることができません。また、底辺×高さのルールが、幸運な底辺の選択に依存しないようにする必要があります。
ほとんどのカリキュラムでは、生徒は8年生までに幾何学的知識の体系的な基礎を持っていません。これらの解剖が機能することの確かな証拠。しかし、直感的な理解は、式を説明して正当化するのに十分であり、後の幾何学的研究のための良い根拠です。
三角形の面積
平行四辺形の面積を見つける方法を知ることは、私たちに役立ちます三角形の領域を見つけます。
三角形を解剖する
三角形を平行にスライスすることで、三角形を2つの部分（1つは三角形、もう1つは台形）に解剖できます。ベースに。そのスライスで高さを正確に半分にカットすると、2つの部分が合わさって、同じ底辺で半分の高さの平行四辺形が作成されます。
つまり、底辺×半分の高さは三角形の面積を示します。同様の解剖は、ハーフベース×高さを示しています。どちらも
bhになります。
三角形を2倍にして、結果の領域を半分にします
別の考え方：2つのコピー三角形は、三角形と同じ底辺と同じ高さの平行四辺形を作成します。
平行四辺形の面積は底辺×高さ、ただし、これは三角形の面積の2倍であるため、解剖法で見たように、三角形の面積は底辺×高さのになります。
（いつものように） 、「ベース」を選択し、ベースから反対側の頂点まで、そのベースに垂直な高さを測定します。）
台形の領域
台形を2倍にして、結果の領域を半分にします。
三角形の場合と同様に、平行四辺形の2つのコピーを組み合わせて平行四辺形を作成できます。
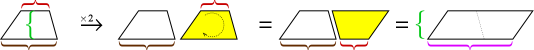
平行四辺形の高さは台形の高さと同じですが、その底辺は台形の2つの底辺の合計です。したがって、平行四辺形の面積は高さ×（base1 + base2）です。しかし、その領域は2つの台形であるため、台形の領域を取得するには、半分にカットする必要があります。
台形の解剖
また、解剖した方法で台形を解剖することもできます。三角形。1つのスライスで高さが半分になります。 2つの部分が合わさって、台形の2つの底辺の合計が底辺であるが、高さが台形の高さの半分である平行四辺形を作成します。
台形の場合、底辺はできません。自由に選ばれます。 2つの平行な辺は底辺であり、高さは、いつものように、一方の底辺から反対側への垂直距離です。
この平行四辺形の面積は、高さ（台形の半分の高さ）に底辺（台形の底辺の合計）を掛けたものであるため、面積は半分の高さ×（base1 + base2）になります。平行四辺形は台形とまったく同じ「もの」から作られているので、それも台形の面積です。
どちらにしても、台形の面積は×高さ×（base1 + base2）。
他の特別な四辺形の面積
ひし形の面積
ひし形の面積は、断片を切り取って並べ替えて平行四辺形を形成することで見つけることができます。これはいくつかの方法で行うことができます。
- 短い対角線（a）を横切って、2つの合同な三角形を形成します。三角形の下半分を上半分の隣に移動して、平行四辺形を形成します。短い方の対角線（a）が平行四辺形のベースになり、長い方の対角線（b）の半分が平行四辺形の高さになります。したがって、ひし形の面積は、* bまたは対角線の積であり、これはひし形の標準式です。
- もう1つの同様の方法は、ひし形を4つの合同三角形にカットし、短い対角線を基部とし、長い対角線の半分を高さとする長方形に再配置することです。
- カット後ひし形を2つの合同三角形に分割すると、三角形の1つの面積を計算できます。これは *底辺（a）*高さ（ b）=
ab。次に、2つあるので2を掛けます。2* ab = ab。
カイトの面積
カイトの面積は、ひし形の面積と同様に見つけることができます。長い対角線を横切ると、2つの合同な三角形が生成されます。それらを並べ替えると、長い対角線（b）を底辺とし、短い対角線（a）の半分を高さとする平行四辺形を形成できます。したがって、面積はb * a = abになります。より複雑なアプローチには、少し代数が含まれます。短い対角線を横切ってカイトをカットし、短い対角線（a）をベースとして2つの三角形を形成します。したがって、最初の三角形の面積は a * squigglyです。ここで、squigglyは高さです。 2番目の三角形の面積は a *（b – squiggly）です。ここで、（b – squiggly）は長い対角線の残りの部分です。したがって、総面積は（ a * squiggly）+（ a *（b – squiggly））になります。 aを因数分解すると、 a（squiggly + b – squiggly）= ab。
まあ、あなたは何を知っていますか。基本的には、平行四辺形の面積の式を知ってから、他の領域の式を導き出すだけです。