ポアソン分布
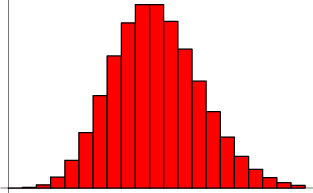
ポアソンプロセスを考えると、
の試行で正確にの成功を得る確率は、二項分布の制限によって与えられます
 |
（1）
|
予想される成功数の関数としての分布の表示
 |
（2）
|
サンプルサイズの代わりに
固定
の場合、式（2）は次のようになります
 |
（3）
|
サンプルサイズ
を大きくすると、分布は近づきます
 |
 |
 |
（4）
|
 |
 |
 |
（5）
|
 |
 |
 |
（6）
|
 |
 |
 |
（7）
|
 |
 |
 |
（8）
|
これはポアソン分布として知られています（Papoulis 1984、pp。101and 554; Pfeiffer and Schum 1973、p。 200）。サンプルサイズ
は、確率関数から完全に脱落していることに注意してください。確率関数は、
のすべての値に対して同じ関数形式です。
ポアソン分布はWolframLanguageにPoissonDistributionとして実装されています。
予想どおり、ポアソン分布は、確率の合計が1になるように正規化されています。
 |
（9 ）
|
確率の比率は次の式で与えられます
 |
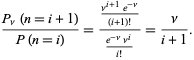（10）
|
ポアソン分布は
where はオイラーの定数であり、
は調和数であり、超越方程式になります
 |
（12）
|
では正確に解くことができません。
Poisson分布のモーメント生成関数は次の式で与えられます
 |
 |
 |
（13）
|
 |
 |
 |
（14）
|
 |
 |
 |
（15）
|
 |
 |
 |
（16）
|
 |
 |
 |
（17）
|
 |
 |
 |
（18）
|
so
 |
 |
 |
（19）
|
 |
 |
 |
（20）
|
（Papoulis 1984、p。 554）。
生のモーメントは、合計によって直接計算することもできます。これにより、ベル多項式
および第2種のスターリング数との予期しない接続が生成されます。
 |
（21）
|
Dobińskiの式として知られています。したがって、
 |
 |
 |
（22）
|
 |
 |
 |
（23）
|
 |
 |
 |
（24）
|
中心モーメントは次のように計算できます
 |
 |
（25）
|
|
 |
 |
 |
（26）
|
 |
 |
 |
（27）
|
したがって、平均、分散、スキューネス、およびクルトシス過剰は
 |
 |
 |
（28）
|
| |
 |
 |
（29）
|
 |
 |
 |
（30）
|
 |
 |
 |
（31）
|
 |
 |
 |
（32）
|
Poissondistributionの特徴的な関数は
（Papoulis 1984、pp。154and 554）であり、累積生成関数は
 |
（34）
|
so
 |
（35）
|
ポアソン分布の平均偏差は次の式で与えられます
 |
（36）
|
ポアソン分布は、
 |
（37）
|
 |
（38）
|
2つの変数のポアソン分布のモーメント母関数は、次の式で与えられます。
 |
（39）
|
独立変数
の場合、
、…、
にはパラメーター
、
、..のポアソン分布があります。、
、次に
 |
（40）
|
パラメータ付きのポアソン分布があります
 |
（41）
|
これは、累積生成関数が
 |
（42）
|
 |
（43）
|
ポアソン分布の一般化は、Saslaw（1989）によってモデル化に使用されています。宇宙で観測された銀河のクラスター化。この分布の形式は、
 |
（44）
|
ここで
は、ボリューム内の銀河の数です
、
、
は銀河の平均密度であり、
は、
が運動エネルギーに対する重力エネルギーの比率です。特異な運動のエネルギー、
が与える
 |
（45）
|
これは確かに
のポアソン分布です。同様に、
に
を付与することもできる。