Misurazione: scoperta di formule per area

Formule area

Studenti che hanno la nozione informale che larea è la “quantità di 2-D “roba” ”contenuta allinterno di una regione può inventare da sé la maggior parte delle formule che spesso gli viene chiesto semplicemente di memorizzare. Ogni formula che reinventano aiuta a rafforzare la loro comprensione (e memoria) per le altre formule che conoscono. (Vedi anche area della superficie.)

Area dei rettangoli

Scegliendo un quadrato come unità dellarea, abbiamo unidea intuitiva dellarea dei rettangoli. Se decidiamo che larea di questo quadrato è 1, un rettangolo 7 volte più lungo avrebbe 7 × 1 come la sua area.

Un rettangolo alto il doppio di avrà il doppio della sua area, quindi larea di è 2 × 7 unità di area. Possiamo contare le due file di sette quadrati. Allo stesso modo, ha 3 righe di 7 quadrati (o 7 colonne di 3 quadrati), per un totale di 7 × 3 quadrati, quindi la sua area è di 21 unità quadrate.

Il numero di quadrati in una riga è la lunghezza del rettangolo. Il numero di righe è laltezza del rettangolo. Quindi larea è lunghezza × altezza.

Poiché un rettangolo può essere disegnato obliquamente, “altezza” è definita come “la direzione perpendicolare alla base” e “base” è definita come, beh, qualunque sia il lato che scegli.

Funziona per contare i numeri. Funziona anche per le frazioni. 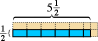Il rettangolo blu mostrato qui misura la metà unità di lunghezza alta per cinque unità e mezza di larghezza. Se scegliamo il quadrato corrispondente come unità di area, vediamo che il rettangolo blu contiene cinque mezze unità di area e un quarto di area, o un totale di due e tre quarti di unità di area. (Le parti rosa mostrano il completamento di ciascuna unità di area quadrata.)

Per includere tutti i numeri, definiamo larea di un rettangolo come base × altezza (dove “base” e “altezza” indicano le lunghezze di quei lati, misurate nelle stesse unità).

Area dei parallelogrammi

Ottenere lidea

Possiamo calcolare una formula per larea di un parallelogramma mediante dissezione ing il parallelogramma e riorganizzando le parti per formare un rettangolo. Poiché il parallelogramma e il rettangolo sono composti dalle stesse parti, hanno necessariamente la stessa area. (Vedi la definizione di area per ulteriori informazioni sul motivo per cui queste aree sono uguali.)

Possiamo vedere che hanno anche esattamente la stessa lunghezza di base (blu) e esattamente la stessa altezza (verde). Poiché base × altezza fornisce larea del rettangolo, possiamo usare le stesse misurazioni sul parallelogramma per calcolare la sua area: base × altezza. (Come prima, “altezza” è misurata perpendicolarmente alla base e “base” è il lato che hai scelto per primo. Vedi parallelogramma.)

Il taglio mostrato sopra rende facile vedere che la lunghezza della base è invariato. In effetti, il taglio perpendicolare può essere eseguito ovunque lungo la base.

Puntellamento dei fori

Intuizione e dimostrazione

Questa dissezione fornisce una comprensione intuitiva della formula dellarea per un parallelogramma, una ragione per cui dovrebbe essere quello che è. Ma non abbiamo messo in dubbio se la dissezione “funziona davvero”. Cioè, quando tagliamo il parallelogramma e ne riorganizziamo le parti, ci aspettiamo di ottenere e il risultato è certamente così. Ma le apparenze possono ingannare. Cosa ci assicura che quando spostiamo quel triangolo, il risultato è un rettangolo? E se fosse più simile a (anche se meno esagerato)? Se il risultato non è sempre un rettangolo perfetto, non possiamo utilizzare la nostra conoscenza della formula dellarea del rettangolo per sviluppare una formula per il parallelogramma. Al liceo, gli studenti saranno in grado di dimostrare che le due parti del parallelogramma, una volta riassemblate correttamente, formano un rettangolo . Nelle classi K-8, per la maggior parte, gli studenti devono fare affidamento sullesperimento visivo e ottenere una sensazione intuitiva. Ulteriori informazioni sul motivo per cui funzionano queste dissezioni.

E se scegliamo il lato corto come base?

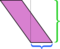
Siamo liberi di scegliere qualsiasi lato come base; “altezza” è definito essere misurata perpendicolarmente al lato che scegliamo come base. Se prendiamo il lato corto (blu) come base, la dissezione mostrata sopra non è così convincente. Tagliare lungo quellaltitudine e riorganizzare le parti lascia un pasticcio:

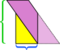
In questo particolare esempio, possiamo salvare il pasticcio facendo un altro taglio, 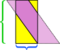ma cosa succederebbe se il parallelogramma fosse ancora più lungo e sottile?

Si scopre che qualsiasi parallelogramma, non importa quanto lungo e sottile, può essere sezionato in questo modo in modo che le parti, forse molte di esse, possano essere riorganizzate in un rettangolo. Ma ci vuole più lavoro per dimostrare che questo può sempre essere fatto. Abbiamo bisogno di unaltra idea.

Unidea di dissezione leggermente diversa rende la vita molto più facile in questo caso. (Da solo, puoi dimostrare che funziona anche nella custodia originale.)

• Racchiudi il parallelogramma in un rettangolo.
• Le due parti del rettangolo che non si trovano allinterno del parallelogramma sono triangoli congruenti.
• Fai scorrere uno di questi triangoli verso laltro finché non si incontrano per formare un rettangolo. 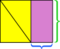Poiché larea totale del rettangolo esterno non è cambiata (è lo stesso rettangolo di prima) e larea gialla non è cambiata (i pezzi si sono semplicemente spostati), la differenza tra loro – le aree viola – devono essere le stesse. Come prima, possiamo anche vedere che le dimensioni dellarea viola rettangolare sono la base e laltezza del parallelogramma originale.

Intuizione e dimostrazione, ripresa : Anche in questo caso, la dissezione fornisce le informazioni essenziali, ma ci vuole un po più di lavoro per assicurare che i due triangoli gialli, che certamente sembrano combaciare per formare un rettangolo, si adattano davvero con precisione, e non solo quasi.

Perché è importante essere così attenti?

Quando creiamo altre formule di area (sotto), vorremo usare il nostro metodo per trovare larea di un parallelogramma, e quindi vogliamo per poter fare affidamento sulla regola che abbiamo trovato. Possiamo essere sicuri che riorganizzare le parti non cambia larea: cioè, dopotutto, è come definiamo larea. Ma dobbiamo anche essere sicuri che le parti combacino come affermiamo, altrimenti non possiamo fare affidamento sulle misurazioni che abbiamo effettuato. E dobbiamo essere sicuri che la regola base × altezza non dipenda da una scelta fortunata della base.

Nella maggior parte dei curricula, gli studenti non hanno una base sufficientemente sistematica di conoscenza geometrica prima della elementare 8 per fare prova del suono che queste dissezioni funzionano. Ma la comprensione intuitiva è sufficiente per spiegare e giustificare le formule e una buona base per un successivo studio geometrico.

Area del triangolo

Sapere come trovare larea di un parallelogramma ci aiuta trova larea di un triangolo.

Dissezione del triangolo

Possiamo sezionare il triangolo in due parti – una di esse un triangolo e una di esse un trapezio – tagliandolo parallelamente alla base. Se tagliamo laltezza esattamente a metà con quella fetta, le due parti si incastrano per formare un parallelogramma con la stessa base ma metà dellaltezza.

Quindi base × mezza altezza fornisce larea del triangolo. Una dissezione simile mostra mezza base × altezza. Entrambi si riducono a bh.

Raddoppiando il triangolo e quindi dimezzando larea risultante

Un altro modo di pensare: due copie di il triangolo forma un parallelogramma con la stessa base e la stessa altezza del triangolo.

Larea del parallelogramma è base × altezza, ma è il doppio dellarea del triangolo, quindi larea del triangolo è di base × altezza, come abbiamo visto con il metodo di dissezione.

(Come sempre , scegli una “base” e misura laltezza perpendicolare a quella base, dalla base al vertice opposto.)

Area del trapezio

Raddoppiando il trapezio e poi dimezzando larea risultante

Come era vero con il triangolo, due copie di un trapezio possono essere combinate per formare un parallelogramma.

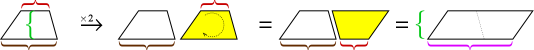
Laltezza del parallelogramma è uguale allaltezza del trapezio, ma la sua base è la somma delle due basi del trapezio. Quindi larea del parallelogramma è altezza × (base1 + base2). Ma quellarea è composta da due trapezi, quindi dobbiamo tagliarla a metà per ottenere larea del trapezio.

Sezionare il trapezio

Potremmo anche sezionare il trapezio nel modo in cui labbiamo sezionato il triangolo, con una sola fetta che ne taglia a metà laltezza. Le due parti si incastrano per formare un parallelogramma la cui base è la somma delle due basi del trapezio, ma la cui altezza è la metà dellaltezza del trapezio.

Nel caso del trapezio, le basi non possono essere scelto a piacimento. I due lati paralleli sono le basi e laltezza, come sempre, è la distanza perpendicolare da una base allaltra.

Larea di questo parallelogramma è la sua altezza (metà altezza del trapezio) moltiplicata per la sua base (somma delle basi del trapezio), quindi la sua area è metà altezza × (base1 + base2). Poiché il parallelogramma è composto esattamente dalla stessa “materia” del trapezio, questa è anche larea del trapezio.

In ogni caso, larea del trapezio è × altezza × (base1 + base2).

Area di altri quadrilateri speciali

Area del rombo

Larea di un rombo può essere trovata tagliando e riorganizzando i pezzi per formare un parallelogramma. Questo può essere fatto in diversi modi:

1. Tagliare la diagonale più corta (a) per formare due triangoli congruenti. Sposta la metà inferiore del triangolo accanto alla metà superiore per formare un parallelogramma. La diagonale più corta (a) diventa la base del parallelogramma e metà della diagonale più lunga (b) diventa laltezza del parallelogramma. Pertanto, larea del rombo è un * bo il prodotto delle diagonali, che è la formula standard per il rombo.
2. Un altro modo simile è tagliare il rombo in quattro triangoli congruenti e riorganizzarli in un rettangolo con la diagonale più corta come base e metà della diagonale più lunga come altezza.
3. Dopo il taglio il rombo in due triangoli congruenti, possiamo calcolare larea di uno dei triangoli, che è * base (a) * altezza ( b) = ab. Quindi moltiplica per due poiché ce ne sono due: 2 * ab = ab.

Area dellaquilone

Larea di un aquilone può essere trovata simile allarea di un rombo. Tagliando la diagonale più lunga si ottengono due triangoli congruenti. Se li riorganizziamo, possiamo formare un parallelogramma con la diagonale più lunga (b) come base e metà della diagonale più corta (a) come altezza. Quindi, larea diventa b * a = ab. Un approccio più complicato richiede un po di algebra. Taglia laquilone lungo la diagonale più corta per formare due triangoli con la diagonale più corta (a) come base. Quindi larea del primo triangolo è a * ondulato, dove ondulato è laltezza. Larea del secondo triangolo è a * (b – ondulato), dove (b – ondulato) è la parte rimanente della diagonale più lunga. Larea totale diventa quindi ( a * ondulato) + ( a * (b – ondulato)). Scartando a, abbiamo a (ondulato + b – ondulato) = ab.

Ebbene, che ne sai. Fondamentalmente, devi solo conoscere la formula per larea di un parallelogramma e quindi derivare la formula per gli altri.