Distribuzione Poisson
Dato un processo di Poisson, la probabilità di ottenere esattamente 
successi in 
prove è data dal limite di una distribuzione binomiale
 |
(1)
|
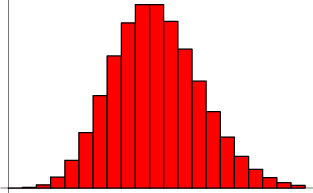
Visualizzazione della distribuzione in funzione del numero di successi previsto
 |
(2)
|
invece della dimensione del campione 
per 
fisso, lequazione (2) diventa
 |
(3)
|
Se la dimensione del campione 
diventa grande, la distribuzione si avvicina a
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
nota come distribuzione di Poisson (Papoulis 1984, pp. 101 e 554; Pfeiffer e Schum 1973, p. 200). Tieni presente che la dimensione del campione 
è stata completamente esclusa dalla funzione di probabilità, che ha la stessa forma funzionale per tutti i valori di 
.
La distribuzione di Poisson è implementata in WolframLanguage come PoissonDistribution.
Come previsto, la distribuzione di Poisson è normalizzata in modo che la somma delle probabilità è uguale a 1, poiché
 |
(9 )
|
Il rapporto delle probabilità è dato da
 |
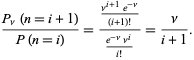(10)
|
La distribuzione di Poisson raggiunge un massimo quando
 |
(11)
|
dove è la costante di Eulero-Mascheroni e 
è un numero armonico, che porta allequazione trascendentale
 |
(12)
|
che non può essere risolto esattamente per 
.
La funzione di generazione del momento della distribuzione Poisson è data da
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
so
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, p. 554).
I momenti grezzi possono anche essere calcolati direttamente per sommatoria, il che produce una connessione inaspettata con il polinomio di Bell 
e i numeri di Stirling del secondo tipo
 |
(21)
|
nota come formula di Dobiński “.Pertanto,
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
I momenti centrali possono quindi essere calcolati come
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
quindi la media, la varianza, lasimmetria e leccesso di curtosi sono
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
La funzione caratteristica per Poissondistribution è
(Papoulis 1984, pp. 154 e 554), e la funzione di generazione di cumulanti è
 |
(34)
|
so
 |
(35)
|
La deviazione media della distribuzione di Poisson è data da
 |
(36)
|
La distribuzione di Poisson può anche essere espressa in termini di
 |
(37)
|
 |
(38)
|
La funzione di generazione del momento di una distribuzione di Poisson in due variabili è data da
 |
(39)
|
Se le variabili indipendenti 
, 
, …, 
hanno distribuzioni di Poisson con parametri 
, 
, …, 
, quindi
 |
(40)
|
ha una distribuzione di Poisson con parametro
 |
(41)
|
Questo può essere visto poiché la funzione di generazione di cumulanti è
 |
(42)
|
 |
(43)
|
Saslaw (1989) ha utilizzato una generalizzazione della distribuzione di Poisson per modellare il raggruppamento osservato delle galassie nelluniverso. La forma di questa distribuzione è data da
 |
(44)
|
dove 
è il numero di galassie in un volume 
, 
, 
è la densità media delle galassie e 
, con 
è il rapporto tra lenergia gravitazionale e la cinetica energia di movimenti peculiari, Lasciando 
si ottiene
 |
(45)
|
che è effettivamente una distribuzione di Poisson con 
. Allo stesso modo, lasciando 
si ottiene 
.