Distribuzione esponenziale
di Marco Taboga, PhD
La distribuzione esponenziale è una distribuzione di probabilità continua utilizzata per modellare il tempo che dobbiamo aspettare prima che si verifichi un determinato evento. È la controparte continua della distribuzione geometrica, che è invece discreta.
A volte è anche chiamata distribuzione esponenziale negativa.
Introduzione
Quanto tempo passerà prima che si verifichi un terremoto in una determinata regione? Quanto tempo dobbiamo aspettare prima che un cliente entri nel nostro negozio? Quanto tempo ci vorrà prima che un call center riceva la prossima telefonata? Per quanto tempo un macchinario funzionerà senza rompersi?
Domande come queste trovano spesso risposta in termini probabilistici utilizzando la distribuzione esponenziale.
Tutte queste domande riguardano il tempo di cui abbiamo bisogno attendere prima che si verifichi un determinato evento. Se questo tempo di attesa è sconosciuto, è spesso appropriato pensarlo come una variabile casuale con una distribuzione esponenziale.
In parole povere, il tempo 
di cui abbiamo bisogno attendere prima che si verifichi un evento ha una distribuzione esponenziale se la probabilità che levento si verifichi durante un certo intervallo di tempo è proporzionale alla lunghezza di tale intervallo di tempo.
Più precisamente, ha una distribuzione esponenziale se la probabilità condizionale è approssimativamente proporzionale alla lunghezza dellintervallo di tempo compreso tra i tempi e , per qualsiasi istante .
In molte situazioni pratiche questa proprietà è molto realistica. Questo è il motivo per cui la distribuzione esponenziale è così ampiamente utilizzata per modellare i tempi di attesa.
La distribuzione esponenziale è strettamente correlata alla distribuzione di Poisson. Se 1) un evento può verificarsi più di una volta e 2) il tempo trascorso tra due occorrenze successive è distribuito in modo esponenziale e indipendente dalle occorrenze precedenti, il numero di occorrenze dellevento allinterno di una data unità di tempo ha una distribuzione di Poisson. Invitiamo il lettore a vedere la lezione sulla distribuzione di Poisson per una spiegazione più dettagliata e una rappresentazione grafica intuitiva di questo fatto.
Definizione
La distribuzione esponenziale è caratterizzata come segue.
Definizione Sia una variabile casuale continua. Lascia che il suo supporto sia linsieme di numeri reali positivi: Sia . Diciamo che ha una distribuzione esponenziale con il parametro se e solo se la sua funzione di densità di probabilità è Il parametro è chiamato rate parameter.
Una variabile casuale con una distribuzione esponenziale è anche chiamata variabile casuale esponenziale.
Quanto segue è una prova che è una funzione di densità di probabilità legittima.
La non negatività è ovvia. Dobbiamo dimostrare che lintegrale di su è uguale a . Ciò è dimostrato come segue:
Per comprendere meglio la distribuzione esponenziale, puoi dare unocchiata ai suoi grafici di densità.
Il parametro rate e sua interpretazione
Abbiamo menzionato che la probabilità che levento si verifichi tra due date e è proporzionale a (a condizione che non si sia verificato prima del ). Il parametro di velocità è la costante di proporzionalità: dove è un infinitesimale di ordine superiore a (ovvero una funzione di che va a zero più rapidamente di fa).
La condizione di proporzionalità di cui sopra è anche sufficiente per caratterizzare completamente la distribuzione esponenziale.
Proposizione La condizione di proporzionalità è soddisfatto solo se ha una distribuzione esponenziale.
La probabilità condizionale può essere scritta come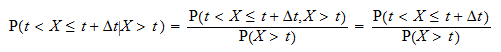 
Indica con la funzione di distribuzione di , ovvero e la sua funzione di sopravvivenza: Quindi, Dividendo entrambi i lati per , otteniamo dove è una quantità che tende a quando tende a . Prendendo i limiti su entrambi i lati, otteniamo o, per definizione di derivata: Questa equazione differenziale è facilmente risolvibile utilizzando la catena regola: Prendendo lintegrale da a di entrambi i lati, otteniamo e o Ma (perché non può assumere valori negativi) implica Esponenziando entrambi i lati, otteniamo Pertanto, o Ma la funzione di densità è la prima derivata della funzione di distribuzione: e il termine più a destra è la densità di una variabile casuale esponenziale. Pertanto, la condizione di proporzionalità è soddisfatta solo se è una variabile casuale esponenziale
Valore atteso
Il valore previsto di una variabile casuale esponenziale è
Può essere derivato come segue: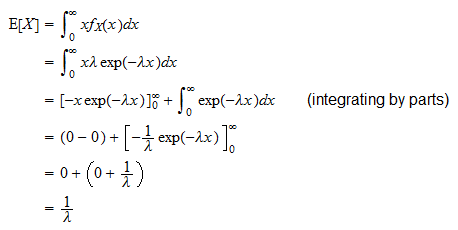 
Varianza
La varianza di un la variabile casuale esponenziale è
può essere derivato grazie alla solita formula di varianza (): 
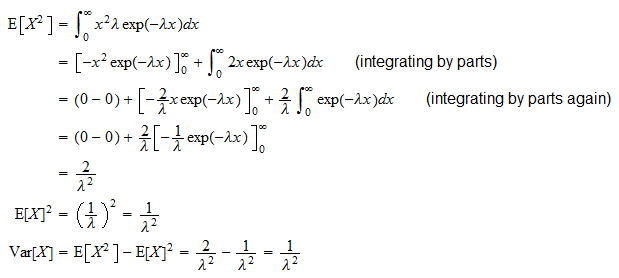
Funzione di generazione del momento
La funzione di generazione del momento di una variabile casuale esponenziale è definita per qualsiasi :
La definizione della funzione di generazione del momento fornisce Di Naturalmente, gli integrali di cui sopra convergono solo se , cioè solo se . Pertanto, la funzione di generazione del momento di una variabile casuale esponenziale esiste per tutti i .
Funzione caratteristica
La funzione caratteristica di una variabile casuale esponenziale è
Usando la definizione di funzione caratteristica e il fatto che possiamo scrivere Ora calcoliamo separatamente i due integrali . Il primo integrale è 
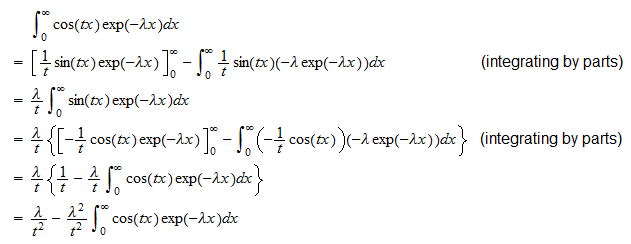Pertanto, che può essere riorganizzato per restituire o Il secondo integrale è 
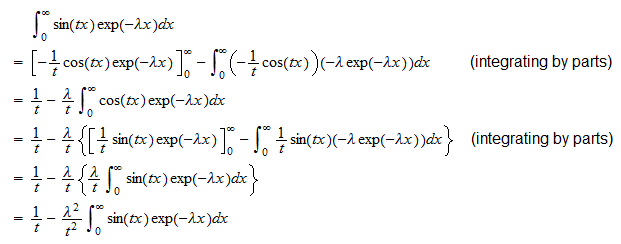Pertanto, che può essere riorganizzato per restituire o Mettendo insieme i pezzi, otteniamo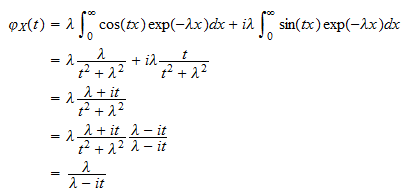 
Funzione di distribuzione
La funzione di distribuzione di una variabile casuale esponenziale è
Se , allora perché non può assumere valori negativi. Se , allora
Ulteriori dettagli
Nelle seguenti sottosezioni puoi trovare maggiori dettagli sulla distribuzione esponenziale.
Proprietà senza memoria
Una delle proprietà più importanti della distribuzione esponenziale è la proprietà senza memoria: per qualsiasi .
Ciò è dimostrato come segue: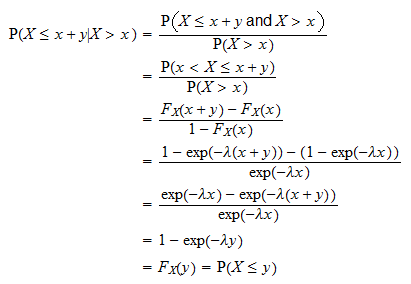 
è il tempo che dobbiamo aspettare prima di un determinato evento si verifica. La proprietà precedente dice che la probabilità che levento si verifichi durante un intervallo di tempo di lunghezza è indipendente da quanto tempo è già trascorso () senza che levento si verifichi.
La somma delle variabili casuali esponenziali è una variabile casuale Gamma
Supponi , , …, sono variabili casuali reciprocamente indipendenti con distribuzione esponenziale con parametro .
Definisci
Quindi, la somma è una variabile casuale Gamma con parametri e .
Questo è dimostrato usando il momento funzioni generatrici (ricorda che la funzione generatrice di momenti di una somma di variabili casuali mutuamente indipendenti è solo il prodotto delle loro funzioni generatrici di momenti): Questultima è la funzione generatrice di momenti di una gamma distribuzione con i parametri e . Quindi ha una distribuzione Gamma, perché due variabili casuali hanno la stessa distribuzione quando hanno la stessa funzione di generazione del momento.
A volte si dice anche che la variabile casuale abbia una distribuzione Erlang. La distribuzione di Erlang è solo un caso speciale della distribuzione Gamma: una variabile casuale Gamma è anche una variabile casuale di Erlang quando può essere scritta come somma di variabili casuali esponenziali.
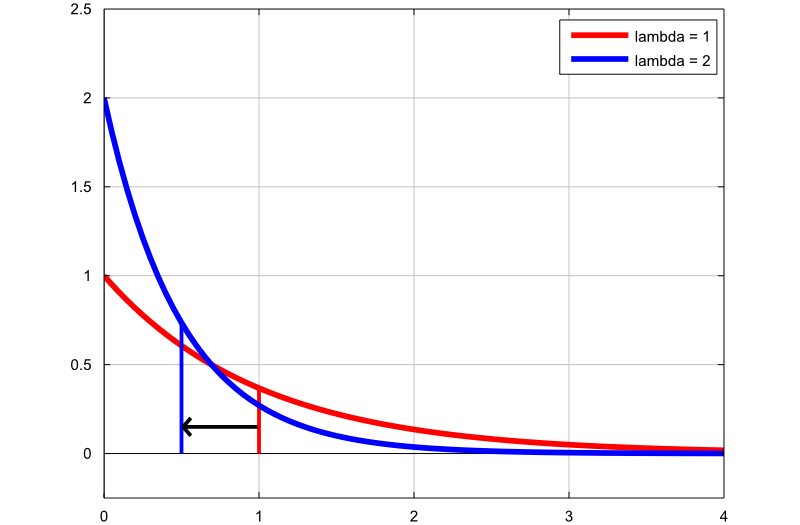
Grafico densità
Il grafico successivo mostra come cambia la densità della distribuzione esponenziale cambiando il parametro della velocità:
-
il primo grafico (linea rossa) è la funzione di densità di probabilità di una variabile casuale esponenziale con parametro di velocità
; -
il secondo grafico (linea blu) è la funzione di densità di probabilità di una variabile casuale esponenziale con parametro di velocità
.
Le sottili linee verticali indicano la media delle due distribuzioni. Tieni presente che, aumentando il parametro rate, diminuiamo la media della distribuzione da a .
Esercizi risolti
Di seguito puoi trovare alcuni esercizi con soluzioni spiegate.
Esercizio 1
Sia una variabile casuale esponenziale con parametro . Calcola la seguente probabilità:
Prima di tutto possiamo scrivere la probabilità come utilizzando il fatto che la probabilità che una variabile casuale continua assuma un valore specifico è uguale a zero (vedi Variabili casuali continue ed eventi a probabilità zero). Ora, la probabilità può essere scritta in termini della funzione di distribuzione di come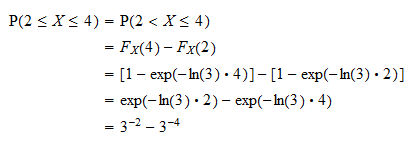 
Esercizio 2
Supponi che la variabile casuale abbia una distribuzione esponenziale con il parametro . Calcola la seguente probabilità:
Questa probabilità può essere facilmente calcolata utilizzando la funzione di distribuzione di :
Esercizio 3
Qual è la probabilità che una variabile casuale è inferiore al valore previsto, se ha una distribuzione esponenziale con il parametro ?
Il valore previsto di una variabile casuale esponenziale con parametro è La probabilità di cui sopra può essere calcolata utilizzando la funzione di distribuzione di :
Come citare
Si prega di citare come: