Come calcolare larea
Calcolare larea
Larea viene misurata in quadrati (o unità quadrate).
Quanti quadrati ci sono in questo rettangolo?

Possiamo contare i quadrati o possiamo prendi la lunghezza e la larghezza e usa la moltiplicazione. Il rettangolo sopra ha unarea di 15 unità quadrate.
Larea di un rettangolo è = lunghezza x larghezza
Esempi di calcolo dellarea di un rettangolo
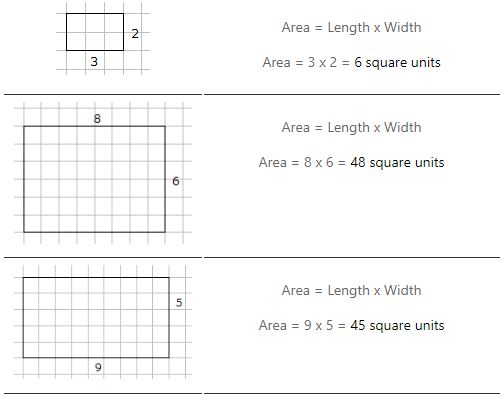
Unità di misura dellarea
Misuriamo larea usando i quadrati. Utilizziamo quadrati di dimensioni diverse a seconda di quanto è grande o piccola unarea.
| Esempio | Lunghezza del lato sui quadrati | Unità |
| Dimensione del unghia sul pollice | Millimetro | mm2 |
| Dimensione del pezzo di carta | Centimetro | cm2 |
| Dimensioni di una stanza | Metro | m2 |
| Dimensioni di una città | Chilometro | km2 |
Non dimenticare il piccolissimo 2
Scriviamo le dimensioni dei quadrati utilizzando un piccolo 2 accanto allunità.
Scriviamo mm2, cm2, m2, km2, cm2
Possiamo dire “63 millimetri quadrati” o “63 millimetri quadrati”
Potremmo utilizzare quadrati piccoli per misurare aree ampie. Lunico problema è che dovremmo usare quadrati molto grandi numeri. Ad esempio, un campo potrebbe essere misurato a 5.000.000.000 di millimetri quadrati quando 5.000 metri quadrati sarebbero una dimensione molto più facile da dire, scrivere e visualizzare.
Probabilmente sentirai più unità per misurare larea; pollici quadrati, piedi quadrati, iarde quadrate, miglia quadrate, acri, ettari sono tutte unità utilizzate per misurare larea.
Altri esempi di calcolo dellarea
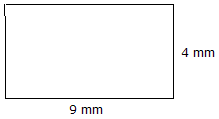 |
Area = Lunghezza x Larghezza Area = 9 mm x 4 mm = 36 mm2 |
 |
Area = Lunghezza x Larghezza Area = 7 cm x 6 cm = 42 cm2 |
 |
Area = Lunghezza x Larghezza Area = 8 mx 2 m = 16 m2 |
 |
Area = Lunghezza x Larghezza Area = 7 km x 5 km = 35 km2 |
Area di un quadrato
La lunghezza e la larghezza di un quadrato sono le stesse, quindi dobbiamo solo moltiplicare la lunghezza per la lunghezza.
| Area = Lunghezza x Lunghezza Area = 6 cm x 6 cm = 36 cm2 |
Area di un cerchio
Larea di un cerchio = πr2
dove r è il raggio del cerchio e π è il rapporto tra la circonferenza di un cerchio e il suo diametro.
π (pronunciato “torta” e spesso scritto “Pi”) è un decimale infinito con un comune approssimazione di 3.14159. Puoi trovare ulteriori informazioni su Pi qui
Esempio di calcolo dellarea di un cerchio
 |
Area = πr2 Area = 3,14159 x (4 cm) 2 Area = 3,14159 x 16 cm2 Area = 50,27 cm2 Risposta arrotondata a 2 cifre decimali |
Spiegazione della formula dellarea di un cerchio
Prendi un cerchio e dividilo in settori di uguale dimensione e riorganizzali come mostrato di seguito. Notare come, man mano che i settori diventano più piccoli, la forma diventa più simile a un rettangolo. Nota: non cè limite a quanto piccoli potrebbero essere questi settori ea quanto potrebbero assomigliare a un rettangolo quando disposti.
Supponendo di sapere che la circonferenza di un cerchio è uguale a 2πr, possiamo aggiungere le dimensioni a il “rettangolo” come mostrato di seguito. Usando larea di una formula di area rettangolo, area = larghezza x altezza possiamo vedere come il nostro cerchio, riconfigurato come un rettangolo, può essere mostrato per avere unarea che si avvicina a πr xr o πr2
Cerchio Settori riorganizzati

Settori circolari riorganizzati – Inizio sembrare un rettangolo

Area di Forme composte
Ci sono molti casi in cui il calcolo di unarea totale richiede il calcolo di più di unarea seguita da unaddizione, una sottrazione o qualche altra combinazione di operazioni per trovare larea richiesta.
Nota: negli esempi seguenti le unità di misura non sono mostrate e le risposte e il valore di π (Pi) sono stati arrotondati al centesimo più vicino.
Esempio: forme composte semplici
Lesempio di calcolo dellarea riportato di seguito è relativamente semplice. La forma può essere vista come un triangolo combinato con un rettangolo.
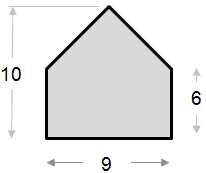 |
Area della parte del triangolo: ½ x base x altezza ½ x 9 x 4 = 18 Area della parte rettangolo: Area totale = 18 + 54 = 72 |
Lesempio precedente illustra un requisito comune quando si lavora con il composto forme – trovare le dimensioni che non vengono mostrate. Quando fai da tutore ai tuoi figli, dai aiuto, quando necessario, per trovare queste dimensioni “mancanti”. Di seguito è riportato un altro esempio.
Ricerca delle dimensioni
 |
Quali sono le dimensioni della parte rettangolare piccola? Larghezza? 12 – 7 – 2 = 3 Altezza? 8 – 6 = 2 |
Esempio: sottraendo unarea da unaltra
Nellesempio seguente, la forma può essere vista come un rettangolo con un triangolo ritagliato.
 |
Area della parte del rettangolo: larghezza x altezza 5 x 6 = 30 Area della parte del triangolo: Area totale = 30 – 4,50 = 25,50 |
Esempio: aree parziali
Lesempio sotto è simile a quello sopra, anche se, poiché abbiamo un semicerchio, dobbiamo calcolare una frazione (metà) dellarea del cerchio. Nota in questo esempio il diametro e non il raggio.
 |
Area della parte del triangolo: ½ x base x altezza ½ x 6 x 6 = 18 Area della parte del semicerchio: Area totale = 18 – 3,53 = 14,47 |
Esempio: decisioni! Combina? Sottrai
È comune disporre di più di un modo per calcolare larea finale. Negli esempi seguenti la forma può essere vista come due rettangoli combinati o come un rettangolo grande con un rettangolo più piccolo “ritagliato” dallangolo in alto a destra.
Fogli di lavoro per larea di calcolo
Stampa estrai i fogli di lavoro elencati di seguito e usali per esercitarti quando fai da tutore ai tuoi figli.
- Calcolo di aree – Rettangoli e quadrati
- Calcolo di aree – Rettangoli
- Calcolo Aree – Rettangoli
- Calcolo di aree composte es con forme rettangolari
- Calcolo di aree composte ad es. con rettangoli, triangoli e cerchi
- Calcolo di aree ad es. di triangoli
- Area di un cerchio
- Calcolo delle aree superficiali, ad es. di prismi rettangolari
Qui troverai più fogli di lavoro sulla geometria stampabili.