Come calcolare il volume

Calcolo del volume

Il volume viene misurato in cubi (o unità cubiche).

Quanti cubi ci sono in questo prisma rettangolare (parallelepipedo)?

Possiamo contare i cubi anche se è più veloce prendere la lunghezza, larghezza e altezza e utilizzare la moltiplicazione. Il prisma rettangolare sopra ha un volume di 48 unità cubiche.

Il volume di un prisma rettangolare è = lunghezza x larghezza x altezza

Esempi di calcolo dellarea di un rettangolo

Dobbiamo fare due moltiplicazioni per calcolare il volume. Calcoliamo larea di una faccia (o lato) e la moltiplichiamo per la sua altezza. Gli esempi seguenti mostrano come ci sono tre modi per farlo.

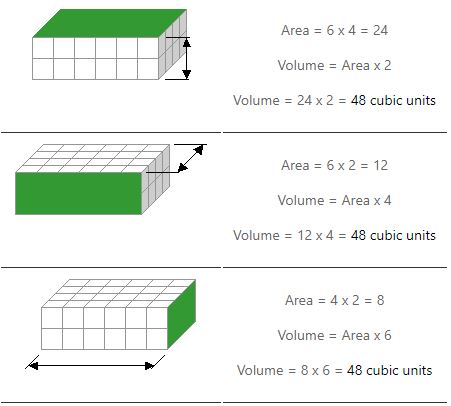
Nota come otteniamo la stessa risposta indipendentemente dal lato che usiamo per trovare unarea.

Quando tuo figlio inizia a lavorare con larea e il perimetro, di solito lavorerà con 2 dimensioni – quadrati, rettangoli, triangoli, ecc. che vengono visualizzati su carta come piatti: non cè profondità o terza dimensione. Lavorare con il volume coinvolge 3 dimensioni. Assicurati che tuo figlio ne sia consapevole e non pensi che i cubi e le altre forme 3D mostrate sulla carta siano semplicemente unaltra “forma sulla pagina”. Mostra loro scatole reali e mostra come queste possono essere disegnate (o rappresentate) su un pezzo di carta bidimensionale. In altre parole, assicurati che la connessione tra ciò che è sulla carta e ciò che rappresenta nel mondo reale sia stabilita.

Assicurati che tuo figlio non sia confuso dalluso del volume usato quando parla di volume .

Unità di misura del volume

Ci sono differenze molto grandi tra le unità di misura del volume. Ad esempio, ci sono 100 centimetri in 1 metro ma ci sono 1.000.000 (sì, 1 milione ) centimetri cubi in un metro cubo.

Perché la grande differenza? Perché in volume non abbiamo solo lunghezza; abbiamo lunghezza, larghezza e altezza. Lesempio di zolletta di zucchero qui sotto lo mostra.

Quanto zucchero? 1 m3 o 1.000.000 cm3

Pensa di riempire una scatola molto grande (sarebbe larga 1 metro, lunga 1 metro e alta un metro) con cubetti di zucchero (con ciascuno lato 1 centimetro).

	Passaggio 1: una riga lungo la parte inferiore della scatola – sarebbe 100 cubetti di zucchero
	Passaggio 2: copri il resto della base della scatola – che darebbe un totale di 100 righe ciascuna con 100 zollette di zucchero. 100 x 100 = 10.000 cubetti zucchero nella parte inferiore della scatola grande.
	Passaggio 3: ripeti 99 volte finché non ci sono strati di 10.000 cubetti impilati 100 in profondità. 10.000 x 100 = 1.000.000 di cubetti di zucchero

Ci sono 1.000.000 cm3 in 1 m3 – fai attenzione a non avere troppo zucchero!

Ci sono altre unità per misurare il volume; pollici cubi, piedi cubi e iarde cubiche sono tutte unità utilizzate per misurare il volume. Millilitri, litri, galloni vengono utilizzati anche soprattutto durante la misurazione dei liquidi.

Non dimenticare i 3 piccolissimi

Scriviamo dimensioni cubiche utilizzando un piccolo 3 accanto allunità.
Scriviamo mm3, cm3, m3, km3, cm3
Possiamo dire “85 centimetri cubi” o “85 centimetri cubi”

Esempi di calcolo del volume di prismi rettangolari

	Volume = Lunghezza x Larghezza x Altezza Volume = 12 cm x 8 cm x 6 cm = 576 cm3
	Volume = Lunghezza x Larghezza x Altezza Volume = 20 mx 2 mx 2 m = 80 m3
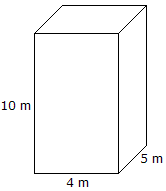	Volume = Lunghezza x Larghezza x Altezza Volume = 10 mx 4 mx 5 m = 200 m3

Volume di un cilindro

Calcolo del volume di un cilindro der comporta la moltiplicazione dellarea della base per laltezza del cilindro. La base di un cilindro è circolare e la formula per larea di un cerchio è: area di un cerchio = πr2. Cè altro qui nellarea di un cerchio.

Volume = Area della base x Altezza Volume = πr2 xh Volume = πr2 h

Nota: negli esempi seguenti useremo 3,14 come valore approssimativo per π (Pi).

Esempio di calcolo del volume di un cilindro

Le dimensioni sono in cm.

Volume = πr2 h Volume = 3.14 x 3 x 3 x 8 Volume = 226,08 cm3

Volume di un cono

Il volume di un cono è uguale a un terzo del volume di un cilindro con altezza e area di base corrispondenti. Questo fornisce la formula per il volume di un cono come mostrato di seguito.

Volume = 1/3 πr2h

Esempio di calcolo del volume di un cono

Le dimensioni sono in cm.

Volume = 1/3 πr2 h Volume = 1/3 x 3,14 x 2 x 2 x 7 Volume = 29,31 cm3

Volume di una sfera

La formula per il volume di una sfera è mostrata di seguito.

Volume = 4/3 πr3

Esempio di calcolo del volume di una sfera

Le dimensioni sono in cm.

Volume = 4/3 πr3 Volume = 4/3 x 3,14 x 4 x 4 x 4 Volume = 267,95 cm3

Fogli di lavoro del volume stampabile

Usa il foglio di lavoro sotto per esercitarti a calcolare i volumi.

• Trovare il volume in unità cubiche – prismi rettangolari e compositi
• Volumi di prismi rettangolari
• Volumi di prismi rettangolari
• Volumi di oggetti del “mondo reale” es. di scatole di cereali
• Calcolo dei volumi ad es. di prismi triangolari e cilindri

Qui otterrai altri fogli di lavoro sulla geometria su perimetro, area e altro ancora.